热膨胀系数的测定介绍

测试技术进入纳米级精度时代的今天,随着科技的进步以及加工手段和测试方法的不断提高,使得一些常见的影响精度的因素,如刀具的磨损、测试仪器的非线性、分辨率低等对于精度的影响大大减小,而对于温度变化引起的性能变化及测量误差却一直无法消除。经过科学家的多年研究,对于控温技术，圆形、方形及球形零件的受温模型已有初步的了解。零件受温后的变形由两方面的因素造成的:一是零件的材料,如相同尺寸的铜棒和铝棒,改变相同温度后,变形量不相等;另一方面是零件的形状,如相同尺寸及材料的铝棒,一个是实心,另一个为有中心孔,改变相同温度,变形量也不相等。因此,为了建立正确的受温变形模型,必须使用材料的微分膨胀系数来计算材料因素引起的确切变形量。工程手册给出的多为平均线膨胀系数,与实际温度下的热膨胀系数值差别较大,满足不了高精度测量及误差修正的需要。研究并给出准确的热膨胀系数,控制减小或尽可能消除温度变化的影响已成为迫切的任务。

热膨胀系数定义为与温度变化相应的样品单位长度上的长度变化。设在t₀℃时,样品的长度为L₀,当温度由t₀℃变为t℃时,其长度为L_t,则有下式成立:

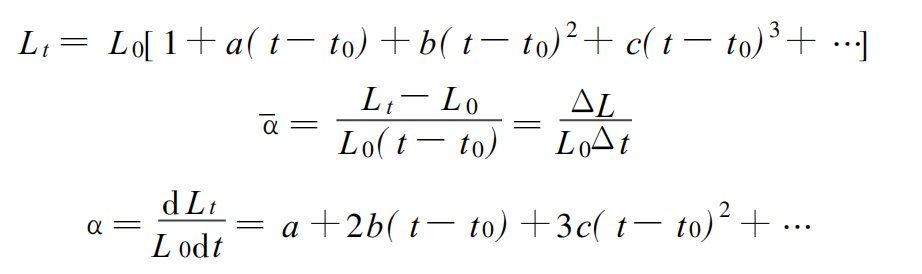
热膨胀系数是温度的函数,随着温度的改变而改变。对于精密测量,如果仅采用手册上给出的平均线膨胀系数进行温度误差计算,将会带来明显的原理误差,必须通过多次测量在一定温度条件下的膨胀量,用最小二乘法拟合一式,再根据三式求得微分膨胀系数。