【摘要】 上面所说的磁化强度起伏和涨落也可以说成是磁化强度矢量在所有方向上“随机跳步”。

当颗粒具有单轴对称的磁各向异性时，微晶颗粒的各向异性能由下式给出:

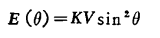
式中，K是各向异性常数，V是颗粒体积，θ是磁化强度方向和易磁化方向的夹角。

当有外场H时,若外场方向沿对称轴方向，那么磁性颗粒的能量由下式给出:

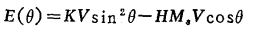
式中，Ms为饱和磁化强度，当H<2K/Ms时，在θ=0、π处有两个最小值。对于外场很大时，θ=π的值不出现。图1给出了H=0时的E(θ)变化图形。可见两个最小值之间，由E=KV的势垒分隔开。

 

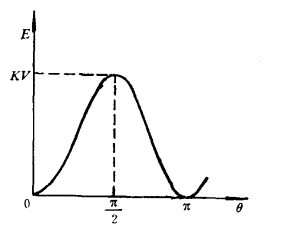
图1 单轴各向异性的能量分布示意图

 

上面所说的磁化强度起伏和涨落也可以说成是磁化强度矢量在所有方向上“随机跳步”。这些方向上都有找到磁化强度矢量的几率，但当分隔两个最小值(或分隔易磁化方向)的各向异性能的势垒KV与热能ƙBT(或外场影响)相比很大时，磁化强度矢量可以认为是固定在易磁化方向中的一个方向上;当KV比ƙBT(或外场影响）较大时，磁化强度矢量可以在对应最小值的方向附近起伏;当KV小于ƙBT时，磁化强度矢量有相当的几率越过分离两个最小值的能垒KV，出现超顺磁驰豫。

超顺磁驰豫频率(τ-1)被定义为磁化强度矢量越过势垒的速率。

朗之万(Langtvin)函数式表明，当单畴微粒足够小时，使得各向异性较小，且远小于外场的影响就会出现超顺磁现象。即在一定温度范围内（根据粒子的尺寸而定)，在外磁场中的行为服从顺磁磁化规律。

 

  • 翁志农. FeNiVSiB非晶态合金结构弛豫、磁各向异性和晶化过程的穆斯堡尔谱学研究[D]. 中山大学, 1991.
  • 王凯, 张毅, 翟亚. 小粒径8Zn0.2Fe2O4纳米颗粒及超顺磁性研究[J]. 化工时刊, 2009.
  • 都有为, 陆怀先, 王挺祥,等. 界面活性剂对Fe_3O_4磁性与穆斯堡尔谱的影响[J]. 物理学报, 1982, 31(010):1417-1422.