【摘要】 拉伸曲线是由拉伸试验机测出的,用来描述材料的应力与应变之间的关系的曲线。
拉伸曲线是由拉伸试验机(图1)测出的,用来描述材料的应力与应变之间的关系的曲线。拉伸曲线可以反映出材料包括弹性变形、塑性变形和断裂这三种基本力学行为的相关信息,可用来综合评定材料各种力学性能,包括强度,塑性,韧性及加工硬化等。在科学研究和实际工程应用中作用显著,因此掌握拉伸曲线分析技巧意义重大。
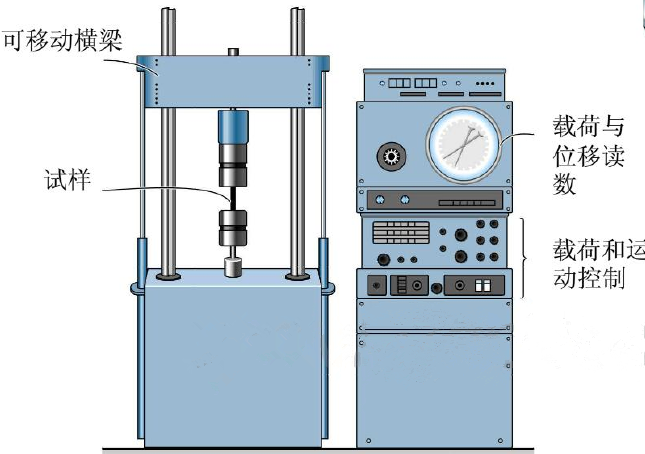
图1. 典型的拉伸试验测试设备.
典型的材料拉伸曲线如图2所示,按照有无屈服平台(橙色椭圆所示:应力与应变一阶导约为零):大致可分为有屈服阶段的拉伸曲线(如建筑钢)和无屈服阶段的拉伸曲线(如高强钢,变形铝合金等)。
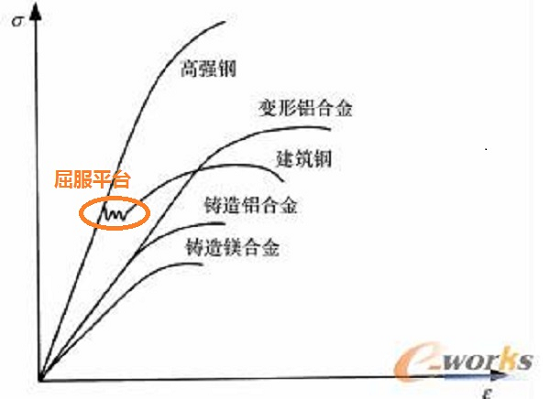
图2. 典型的拉伸曲线(橙色椭圆所示为拉伸屈服平台).
1.拉伸曲线可直接反映的具体信息
比例极限σp:应力与应变成正比关系的最大应力;
弹性极限σe:材料由弹性变形过渡到弹-塑性变形的应力。应力超过弹性极限,开始发生塑性变形时的应力;
屈服极限σs:金属发生明显塑性变形的抗力,屈服点:屈服点对应的强度,有上、下屈服极限;
条件屈服强度σ0.2:当没有明显屈服平台时,规定产生0.2%残余塑性应变时的应力;
抗拉强度(强度极限)σb:试样拉断前最大载荷所决定的临界应力;
弹性模量E:弹性变形阶段,应力和应变成正比例关系(即符合胡克定律),其比例系数即为弹性模量。
延伸率δ:试样拉伸断后标距段的总变形ΔL与原标距长L之比:δ=ΔL/L×100%,和截面收缩率ψ都是描述材料塑性性能的指标。
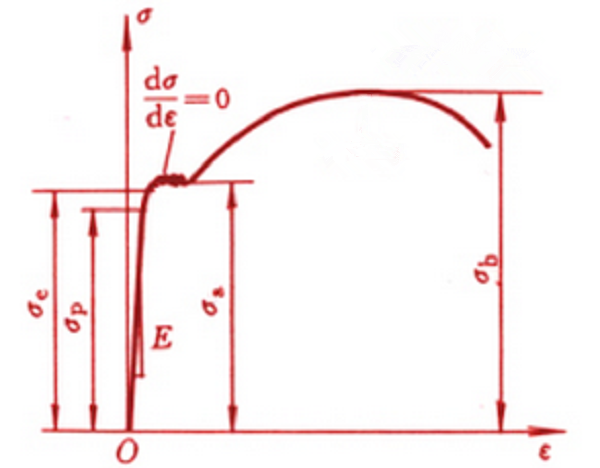
图3. 典型拉伸曲线示意图.
2.拉伸曲线基本特点
材料不同,其拉伸曲线也有所不同,但总的来说:从初始拉伸至最后断裂过程可基本划分为几个特征阶段.
1)弹性阶段:如图4所示,这个阶段分为两种,当应力小于σp 时,应力和应变成正比;超过比例极限后,应力和应变虽然不保持正比关系,但变形依然是弹性的,卸载后变形完全恢复为零,直线斜率E,其大小反映材料抵抗弹性变形的一种能力代表了材料的刚度。此外,材料在发生杆的轴向伸长的同时还发生横向收缩。横向正应变ε与纵向正应变ε之的绝对值μ称为材料的泊松比,反映材料横向变形的弹性常数。
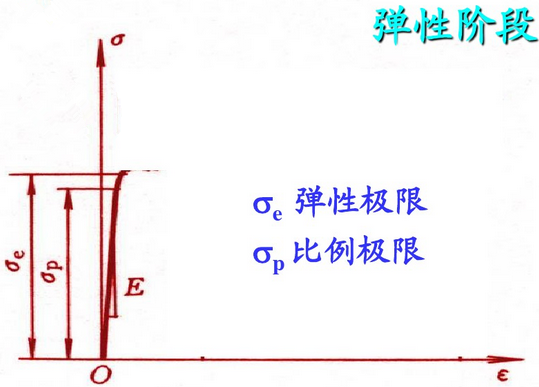
图4. 弹性拉升阶段拉伸曲线示意图.
2)屈服阶段:如图5所示,在超过弹性阶段后出现明显的屈服过程,即曲线沿一水平段上下波动,即应力增加很少,变形快速增加。这表明材料在此载荷作用下,宏观上表现为暂时丧失抵抗继续变形的能力,微观上表现为材料内部结构发生急剧变化。从微观结构解释这一现象是由于构成金属晶体材料结构晶格间的位错,在外力作用下发生有规律的移动造成的。由于材料在这一阶段已经发生过量变形,必然残留不可恢复的变形塑性变形因此,从屈服阶段开始,材料的变形就包含弹性和塑性两部分。
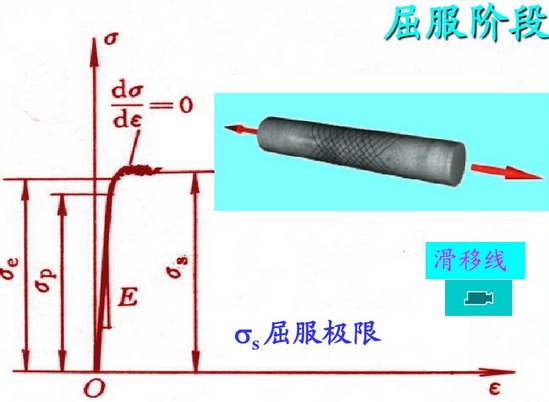
图5. 屈服阶段拉伸曲线示意图.
3)强化阶段:如图6所示,屈服阶段结束后,拉伸曲线又出现上升现象,说明材料恢复了对继续变形的抵抗能力,材料若要继续变形必须施加足够的载荷。如果在这一阶段卸载,弹性变形将随之消失,而塑性变形将永远保留。强化阶段的卸载路径与弹性阶段平行。卸载后若重新加载,材料的弹性阶段线将加长、屈服强度明显提高,塑性将降低。这种现象称作应变强化或冷作硬化,可用来提高材料的强度。强化阶段的塑性变形是沿轴向均匀分布的。拉伸曲线的应力达到强度极限σb,是材料均匀塑性变形的最大抵抗能力,是材料进入颈缩阶段的标志。
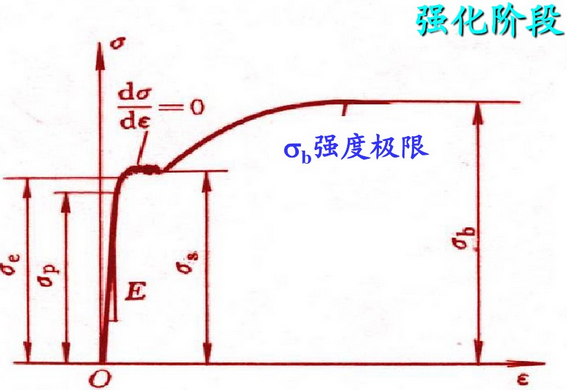
图6. 强化阶段拉伸曲线示意图.
4)颈缩阶段:如图7所示,应力到达强度极限后,开始在试样最薄弱处出现局部变形,从而导致试样局部截面急剧颈缩,承载面积迅速减少,试样承受的载荷很快下降,直至断裂。断裂时,试样的弹性变形消失,塑性变形则遗留在断裂的试样上。
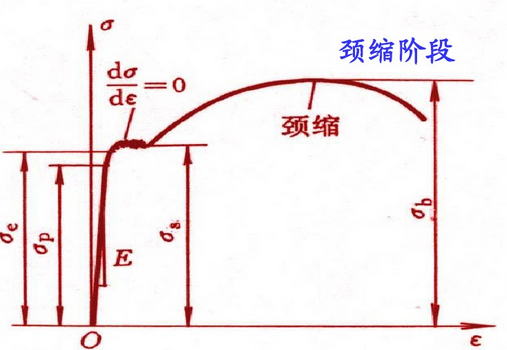
图7. 颈缩阶段拉伸曲线示意图.
3.真实应力应变曲线的处理方法
在设计有关材料结构设计或模拟仿真运算中,经常需要依据材料真实性能参数,而通常通过拉伸实验直接做出来的拉伸曲线,往往是工程上的应力应变曲线,并不能完全精确反映材料的真实拉伸情况(如拉伸实验误差;拉升过程中标距段横截面积的变化等),这就需要对拉伸试验的结果进行处理,得到真实的应力应变曲线。另外,由于实验所得的数据太多,一般为几千个点,甚至为上万个点,而平常仿真软件输入的点一般为几百个,所以为了得到有效数据必须对原始数据进行处理。主要通过以下步骤进行处理(以仿真软件CAE为例):
3.1 对力-位移曲线进行处理
1)清理无效数据
将前面的空白点予以删除,并对位移进行初步的元整,如图8所示,图中的0位移节点,要删除点,直至第一个位移为非0点。
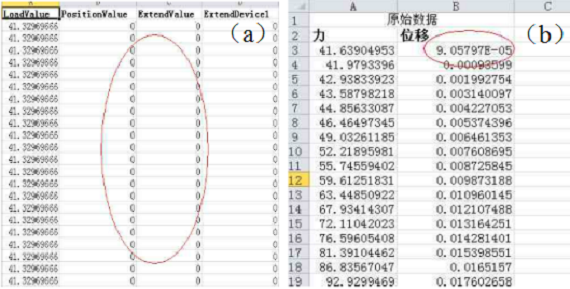
图 8. 无效数据清理前后示意图:(a)清理前;(b)清理后.
2)对位移进行初次处理
位移的数据,小数点后有很多位,首先处理到适当位置就行。
3.2 计算工程应力应变曲线
应力= 力/(厚度*宽度)
应变 = 伸长量/初始长度
3.3 计算真实应力应变曲线
真实应力 = 工程应力*(1+工程应变);
真实应变 = Ln(1+工程应变)
3.4 取整
将应力应变曲线, 进行四舍五入取整。
3.5 筛选数值
以一定应变为增量,取相应的应力值,并绘制折线图,然后取有效区域数值。如图9中的红圈部分为无效区域,应舍去。
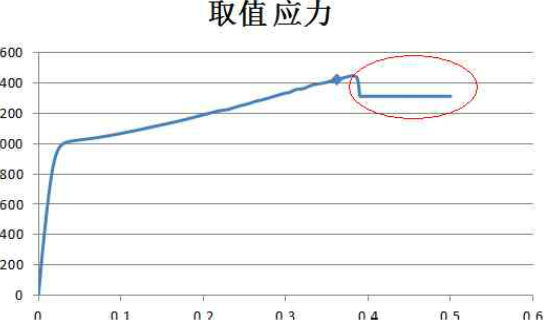
图9. 数值帅选示例(上图中的,红圈部分为无效区域).
3.6有效应力应变
有效应力应变曲线一般是将数据的弹性部分去除,如图10表格所示,直接将(a)中,0.003或0.004之前的对应的应力舍去,应变不变,应力顺移即可获得(b),即:0应变为对应的应力为原来0.004对应的应力,0.002应变对应的应力为原来0.006对应的应力。

图10. 有效应力应变数据处理示例图.
经过以上的处理方法,得到有效应力应变曲线,就可以将得到的数值导入到CAE软件中,进行数值计算。
4.其他处理技巧
1) 当实验测出的位移和力的数值都是从负值开始:
正确的做法不应是直接去除负数值的点,而只保留非负数的点,而应将坐标原点平移,即:将横纵坐标所有值都各自加上测出得到的相应的最大负数值,使各自初始点都从零点开始。
2)严格计算材料延伸率时,是将拉伸总的形变量与原长(标距)的比值计算得到吗?
严格来说,延展率是拉伸塑性形变量与原长(标距)的比值,即:拉伸曲线上进入塑性变形后的总的变形量,减去一开始的弹性变形量才是实际的变形量。通常,工程上,由于弹性变形量相对较小,所以将拉伸总的变形量代替拉伸塑性形变量计算得到的。
3)当遇到拉伸曲线呈特殊情况下应该实验数据取舍问题:如遇到下图11所示,弹性阶段前出现一小段平线。
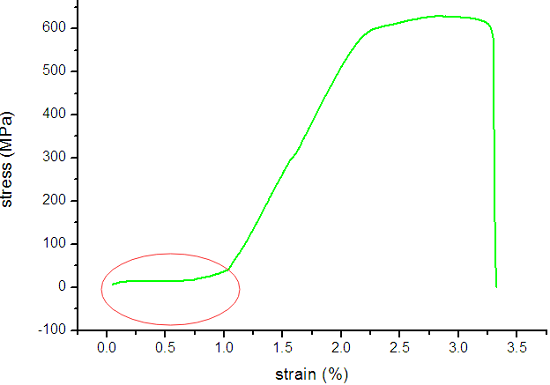
图11. 拉伸弹性阶段前出现一小段平线线的特殊拉伸曲线示例.
该曲线是通过实验计算得到的应力-应变曲线,是真实的,理论上可以用, 前面的平缓区绝大部分是因为夹具系统初始的空隙和试样的弱连接的所致,应该将前面平线段舍弃后重新作图。
【参考文献】
[1]B.C. 伊万诺娃. 金属在拉伸曲线各阶段中进行塑性变形时的几个特点[J]. 金属学报,1958,3(4):253-259.
[2]Haahoba, B.C. AH CCCP, T.XCIY, No 2, 1954.
[3]Poahhckhb, B.M., Makeeba, B.N., Nbecthh AH CCCP OTH, No10, 1954.
[4]金属力学性能---金属拉伸性能,哈尔滨工业大学(网址:http://www.doc88.com/p-237794384927.html ).
[5]真实应力---应变曲线拉伸实验 (网址:http://www.doc88.com/p-933465673926.html ) .
科学指南针提供各类科研测试服务,愿您总能获得想要的结果。我们收到的测试样品来自各地,种类繁多,如果我们回复不及时,还请再次联系,或直接语音电话联络,若您对我们的服务不满意,或对测试结果有疑问,请果断联系我们或直接拨打400-831-0631,我们对每个数据及结果,会负责到底!科研可能很苦,但坚持一定很苦,愿您顺利!
免责声明:部分文章整合自网络,因内容庞杂无法联系到全部作者,如有侵权,请联系删除,我们会在第一时间予以答复,万分感谢。











 您已经拒绝加入团体
您已经拒绝加入团体

 2021-11-08
2021-11-08
 4566
4566
 0
0











