纳米流体的比热容计算（三）

2012年，Pakdaman等基于最小二乘法建立了导热油基MWCNT纳米流体的比热容计算模型，计算模型如公式（9）所示，它可以较为精确的预测重量浓度为0、0.001、0.002和0.004的导热油基MWCNT纳米流体，在313-343K温度范围内的比热容。

（9）

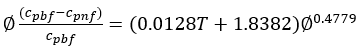
式中: 为纳米流体的比热容，为基液的比热容,T为温度，为质量浓度。

2013年，Sekhar和Sharma在总结了已有文献中8l个水基Al2O3、CuO、SiO2和TiO2纳米流体的实验数据后，建立了回归关系，并且比较了计算值与不同研究人员的实验数据之间的差值，偏差为10%和-8%，从而证实了该表达式的有效性。

（10）

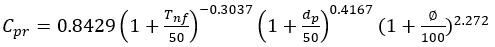
式中:cpr为纳米流体的比热容，Tnf为纳米流体温度，d,为纳米流体粒径，g为纳米颗粒体积分数。

由于纳米颗粒小尺寸效应的影响，导致纳米流体比热容计算与常规的固液两相混合液体的比热容计算存在较大的差异。国内外的专家学者从多个角度对纳米流体比热容的理论计算进行了探讨，发现纳米流体比热容的计算不是简单累加。在实际使用过程中需要根据实际条件选择合适的计算模型，或者通过将部分实验参数简化以适应某模型进行大致计算。通过大量的实验数据发现，温度与比热容之间按照某种规律在一定范围内变化，二者之间存在一定的相关性。处理不同变量之间的关系往往采用回归分析（(Regression analysis)，在不确定性因素之间的联系上可以采用此种统计方法。通过回归分析，可以确定自变量与因变量之间的回归方程。数据处理主要采用基于最小二乘法的一元多项式回归。对于复杂的一元连续函数，可以转化为高阶多项式近似表达。

[1]任龙.高温溴化锂溶液导热系数和比热容的实验测定与模型计算[D].大连理工大学,2015.

[2]Yimin Xuan，Wilfried Roetzel.Conceptions for heat transfer correlation of nanofluids[J].Internati onal Journal of Heat and Mass Transfer, 2000,43(19):3701-3707.

[3]Harry O'Hanley, Jacopo Buongiorno, Thomas McKrell, Lin-wen Hu. Measurement and Model Validation of Nanofluid Specific Heat Capacity with Differential Scanning Calorimetry[J].Advances in Mechanical Engineering,2012,4:1-6.

[4]张琦.基于差示功率补偿的绝热加速量热法研究[D].中国计量大学,2019.

科学指南针提供各类科研测试服务，愿您总能获得想要的结果。我们收到的测试样品来自各地，种类繁多，如果我们回复不及时，还请再次联系，或直接语音电话联络，若您对我们的服务不满意，或对测试结果有疑问，请果断联系我们或直接拨打400-831-0631，我们对每个数据及结果，会负责到底！科研可能很苦，但坚持一定很苦，愿您顺利！