【摘要】 核磁共振成像系统的弥散张量成像介绍

本期我们对核磁共振成像系统的弥散张量成像继续进行介绍。

(1)固定不动的质子的磁矩，在t1-t2以wa率旋转δ的时间。在t3-t4内以wa率反向旋转δ的时间，相位无变化，合成横向磁化矢量Mxy梯度磁场的影响。

(2)假设有三个水分子刚开始都在A点，在t1-t4，一个在A点固定不动，第二个由A点弥散到B点,第三个弥散到C点。加完梯度磁场后，则第-个水分子中质子的磁矩由于两个极性相反的梯度脉冲带来的相位变化相互抵消，因而相位不变。假设δ极短，第二个在t1-t2期间内以wa旋转。在t3-t4内以wb反向旋转，相位发生变化。同理，第三个在t3-t4。期间内以wc反向旋转，其相位也发生变化，如图1和图2所示。在图1和图2中，磁矩的变化从左到右分别为刚开始时，t1-t2期间，t3-t4期间，以及最后的情况。

 

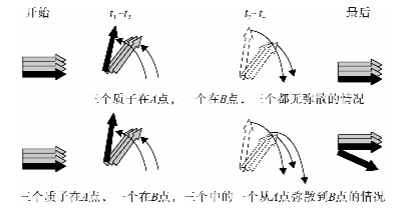
图1 三个在A点的质子及-一个在B点的质子在梯度磁场作用下的有无弥散的情况

 

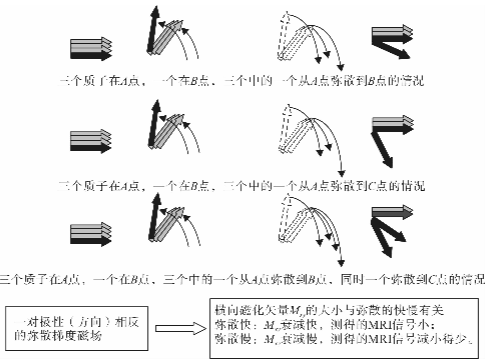
图2三个在A点的质子及-一个在B点的质子在梯度磁场作用下的不同弥散的情况

 

因为wc>wb>wa,这三个质子的磁矩在加完梯度磁场后相位不一致，导致其合成总磁化矢量M.变小。在这两个反向的梯度磁场作用下，由许许多多的水分子中质子磁矩合成的总横向磁化矢量Mxy,因水分子沿梯度磁场的方向弥散而变小。若MRI信号变得越小，则说明弥散越快。

弥散运动的信号衰减可以用下面的公式来表示:

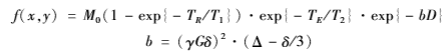
本期由于版面有限，我们将在下一期继续进行向大家介绍关于核磁共振成像的知识。

 

参考文献

[1]赵喜平. 磁共振成像系统的原理及其应用. 科学出版社, 2000.

[2]俎栋林. 核磁共振成像学[M]. 高等教育出版社, 2004.