【摘要】 实验采用三电极体系。选用直径为3.0mm的金电极为工作电极、饱和甘汞电极为参比电极、螺旋状铂丝电极为对电极。
01基本定义
在二茂铁及其衍生物自组装膜的电化学研究实验中,利用CV法,根据Laviron公式来求解转移系数及表观速率常数kapp。
我们将考虑约化O+ne↔R的情形。电势E
E=Ei+vt(1)
在表面电化学中,当服从朗缪尔等温式,O和R被强吸附时,电化学反应只涉及被吸附的分子,如果覆盖度小于1,可以定义表面标准电势E0'[1];它的值由下式给出:
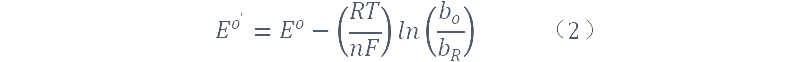
bO和bR是O和R的吸附系数。因此我们可以写成:
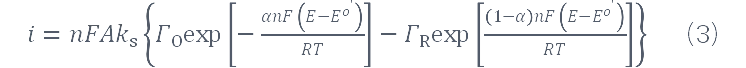


Ks(即kapp)是电化学反应的速率常数(s-1),Гo和ГR是O和R的表面浓度(mol·cm-2),ГT是它们的常数和,A是面积(cm-2)。n、F、α、R和T有它们通常的意义,i在这里用安培表示。电流可由无因次函数:
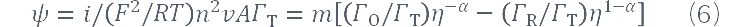
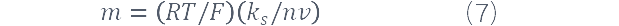
п由等式定义。
通过化简可以得到Laviron公式:
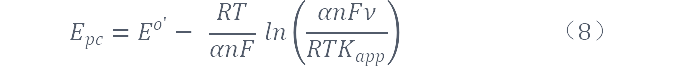
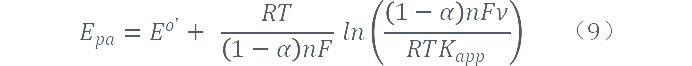
02实验步骤
试剂:H2SO4、HClO4、乙醇、6-(二戊铁基)己硫醇(C16H22FeS,97%)、1-辛硫醇(98%)
仪器:DH7000D电化学工作站
(指南针商城链接:https://mall.shiyanjia.com/product-detail.html?product_id=2123728&category=2)
实验采用三电极体系。选用直径为3.0mm的金电极为工作电极、饱和甘汞电极为参比电极、螺旋状铂丝电极为对电极。
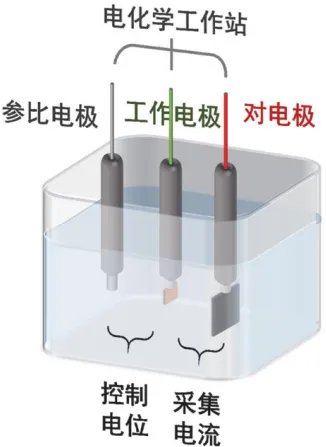
图1 伏安分析实验装置图
1、 打磨金电极。先用直径为0.3μm的Al2O3抛光粉对金电极进行抛光预处理,然后用去离子水清洗干净备用。
2、 金电极的活化。将打磨好的金电极放在0.5MH2SO4体系中进行活化,连接电化学工作站,使用循环伏安方法。设置参数:扫描范围-0.2~1.5V;扫描速度为0.05V/s;扫描圈数为20圈,E、I滤波为100Hz。总共重复3~5次(以出现明显的峰为准),每次实验时需要更换新的硫酸溶液。具体参数如图2。
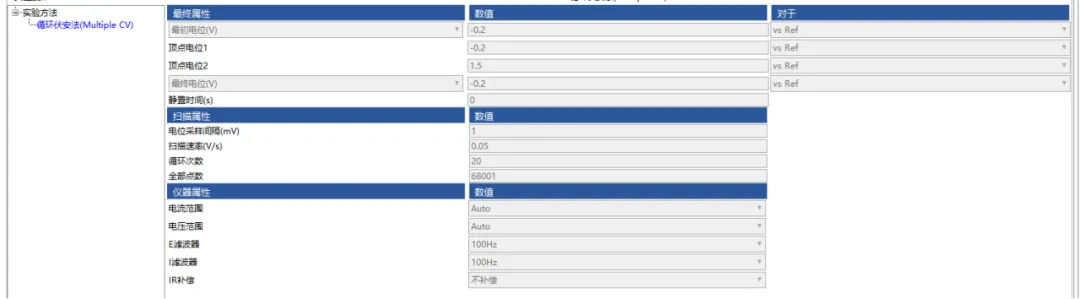
图2 金电极活化时的CV参数
3、 电容计算。选取氧化还原曲线中平缓的部分作为扫描范围,参考范围为0.1~0.3V,更换不同的扫描速度,扫描圈数为2圈,以第2圈为准。
4、金电极的维护。同第二步设置的参数一样。此时需要进行金电极的组装,在组装前金电极需要一直保持活化。待CV曲线扫描至还原曲线末端即将进行氧化反应前,迅速停止扫描将金电极放入组装瓶中。并密封瓶口,组装时间根据目的来定。注意密封时金电极不要触碰到密封瓶(即悬空)。
注意:本实验组装所用溶液,先用0.05mM6-(二戊铁基)己硫醇溶液组装12 h,再用0.05mM 1-辛硫醇溶液组装24h。
5、 将组装完后的金电极放在0.1MHClO4中进行CV表征,扫描范围为0~0.5 V(根据峰形的变化可适当改变范围,保证出现完整的峰形),扫速分别为0.01、0.02、0.05、0.1、0.2、0.5、1、2、5、10、20、50、100、200和500V·s-1。
03数据处理
得到的数据如下图所示
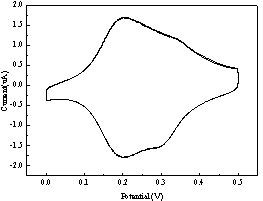
己硫醇溶液中组装12 h后扫速为0.1 V·s-1时在0.1MHClO4中的CV曲线,再在0.05mM1-辛硫醇溶液中组装24h后扫速为0.1V·s-1时在0.1MHClO4中的CV曲线.png)
图3在0.05mM6-(二戊铁基)己硫醇溶液中组装12 h后扫速为0.1 V·s-1时在0.1MHClO4中的CV曲线,再在0.05mM1-辛硫醇溶液中组装24h后扫速为0.1V·s-1时在0.1MHClO4中的CV曲线
如图3左图所示,展示了在0.05mM6-(二戊铁基)己硫醇溶液中组装12小时后,在0.1M HClO4中以扫描速率0.1V·s-1所得到的CV曲线。当只在6-(二戊铁基)己硫醇溶液中组装时,测试出的CV曲线有两个氧化峰和两个还原峰,说明组装膜在表面的分子结构较为复杂,或有多种氧化还原活性中心存在。但是再用1-辛硫醇溶液组装后,CV测试结果如图3右图所示,只出现了一个氧化峰和还原峰,说明使用1-辛硫醇组装的单层膜促进了二戊铁基己硫醇的单层膜的结合,更为简单或具有更高的结构均一性。
.png)
图4 氧化峰峰电位Epa、还原峰峰电位Epc与扫描速率的关系图(横坐标为对数坐标)
如图4所示,当Epa、Epc对扫速的对数作图时,我们发现在扫速小于20V·s-1时,Epa、Epc几乎不随lnv的增加而发生改变。表明该自组装膜体系的电子转移的速率快,是一个电化学可逆的过程。
.png)
图5 氧化峰峰电流Ipa、还原峰峰电流Ipc与扫描速率的关系图(横、纵坐标都为对数坐标)
图5展示了氧化峰电流和还原峰电流与对数扫描速率的关系,随着扫描速率的增加,峰电流显著增加,符合电化学动力学的预期变化。重复循环扫描并未出现电流的衰减(时间间隔在半小时内),说明二茂铁自组装膜在此溶液中的稳定性很好,不受溶液中物种吸附和电荷传递的影响。可认为这些自组装膜的氧化还原中心在溶液中已完全溶剂化,每个氧化还原中心周围的局部环境是均一的。
对曲线进行进一步分析,我们可以通过公式(8)和公式(9)来求转移系数α及表观速率常数kapp。其中,标准气体常数R=8.314J/(mol·K),温度T=298K,法拉第常数F=96487 J/(V·mol)。Eo'是根据Epa、Epc几乎不随lnv的增加而发生改变的那部分扫速下的平衡电势得到的,具体计算步骤如下:
1.分别计算每个扫速下的平衡电势E1o、E2o……Eno。
2.将由第一步求得的n个平衡电势求平均值,即为Eo'。
图6是由氧化还原峰电位数据根据Laviron公式计算得到的曲线。此曲线通过Eo'作为基本线(横轴,Eo'接近0V),然后分别用每个扫速(此时要包括实验所设的所有扫速)下的Epa和Epc与之相减,就得到的了新的氧化还原峰电势,进而可以对其作图,再对非平衡时的数据(图6红线部分)进行拟合,即得图6。
.png)
图6 处理后的氧化峰峰电位Epa、还原峰峰电位Epc与扫描速率的拟合图(横坐标为对数坐标)
将Laviron公式进行变化得:
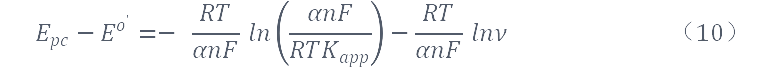
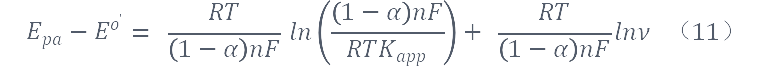
通过上式可求得α及kapp,计算求得α≈0.49,kapp≈3.39×103s-1。
04总结
在求转移系数及表观速率常数时,要注意以下几点:
1、求平衡电势时不是对同一扫速下的氧化还原峰电势进行简单的求平均值,而是要对随扫速变化而氧化还原峰电势基本保持一致时的那部分峰电势进行分别求平衡电势,然后在对求得的各平衡电势进行求平均值,此平均值才是最终的平衡电势,即Eo'。以此平衡电势作为基准线(横轴),然后再用所有扫速下的氧化还原峰电势与Eo'相减,得到新的氧化还原峰电势,再作图、拟合。图6中所求两条斜率(氧化峰所求斜率记为k1,还原峰所求斜率记为k2)分别为(10)式和(11)式中lnv的系数,即
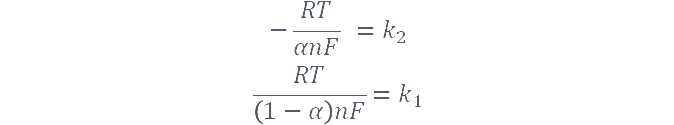
利用k2/k1进行求解,即可求得α。
2、求kapp时,令Epc-Eo'和Epa-Eo'分别等于0,然后再进行分别求解。因通过(10)式和(11)式都可求出kapp,对两者取平均值,即为最终kapp值。另外,对(10)式和(11)式分别求解时,要注意因扫速的变化kapp值也在变化,所以要对每个扫速都进行求kapp,然后再取平均值,分别得到氧化和还原过程中的kapp值,然后对其求平均值,即为最终的kapp。
3、在求解过程中,要注意扫速范围的选取,有些需要全部扫速下的氧化还原峰电势,有些只需要部分扫速下的氧化还原峰电势。
05参考文献
[1] Laviron E .General expression of the linear potential sweep voltammogram in the case of diffusionless electrochemical systems[J].Journal of Electroanalytical Chemistry, 1979, 101(1):19-28.











 您已经拒绝加入团体
您已经拒绝加入团体

 2024-11-12
2024-11-12
 9122
9122
 1
1










