好书解读 | 《模拟计算指南》振动光谱：红外与拉曼光谱

关于本书

01文章介绍

今天我们介绍下《模拟计算指南》的5.1 振动光谱：红外与拉曼光谱。

红外和拉曼都是振动光谱，其谱峰位置对应了一系列振动能级。其中根据振动模式的不同，总体上可分为伸缩振动和弯曲振动两类。前者表现为原子沿着键轴方向的移动，后者对应键角、二面角等围绕着平衡位置的运动。

人们理解红外光谱时借助的最重要模型是谐振子模型。它认为每个振动模式都服从能量规律E=0.5kx²(即相当于经典力学中的胡克定律)，其中k与x分别为力常数和偏离平衡位置的距离。容易知道，力常数即为能量对于位置的二阶偏导。量子化学计算得到能量后，对实空间坐标求二阶偏导，即可得到与振动有关的信息。

宏观世界中的谐振子的最典型例子是我们所熟悉的弹簧。弹簧的长度可以连续取值，但在微观世界中，服从量子力学规律的谐振子的能量只能取到特定的本征值。这一系列本征值对应了每个振动模式的振动能级。当分子处于能量恰好与振动能级之差对应的辐射时(共振条件),分子便会吸收辐射并发生振动能级跃迁。振动能级的能量对应红外波段，因此振动能级之前的跃迁构成了红外和拉曼光谱的基础。

对于频率为w的振动模式，其振动能级本征值为：

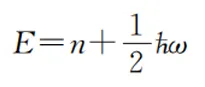
其中，n为自然数；ћ为约化普朗克常数。因此两个相邻振动能级的能量差恰好等于ћw,只与振动频率相关。因此，通过红外光谱测量得到的某个振动模式所对应的红外吸收，就反映了该振动模式的频率。

通常的量子化学程序对分子振动的处理均基于谐振子近似。首先经过结构优化，得到势能面上的极值点结构，随后在频率计算过程中，通过对能量求二阶偏导，得到各振动模式的力常数，再结合其有效质量，得到振动模式的频率。当获得所有振动模式的频率后，就可以知道红外光谱中每个谱峰的位置了。

在已知谱峰位置的基础上，要得到谱图，还需要对其进行适当展宽。在所有的光谱中，共振条件都决定了谱峰的位置，但实际观测到的往往是连续光谱，意味着不满足共振条件的波长处同样会存在一定的吸收，并且吸收强度随着偏离共振条件的程度呈现峰形递降。这是由于分子存在热运动带来的多普勒效应、溶液中还有分子间相互作用带来的能量交换途径，这些因素都导致分子的能级范围变得宽松，从而使得谱峰加宽。谱峰的展宽效应随着体系的性质、光谱测定的条件、仪器结构等而不同，也远不是分子自身的性质所能决定的。因此，如果想要通过计算化学的手段得到分子的光谱，均需在谱峰位置的基础上进行人为展宽，展宽的大小可以任意指定。典型的展宽方式有Gauss型展宽和Lorentz型展宽两种，前者即为常见的正态分布曲线，后者相对而言更为尖锐。计算得到的所有光谱图都是从一组谱峰位置数据的基础上展宽得到的。

通过观察频率计算的输出文件，可以找到各组振动模式的信息。以第四章讨论过的NHC-Ag配合物为例，在频率计算的输出文件中列出了各组振动模式的频率、有效质量、力常数、红外强度等，随后是各振动模式中原子的位移向量(图5.1)。

图5.1NHC-Ag配合物的Gaussian输出文件里频率分析的输出内容(部分)

使用GaussView打开输出文件，右键Results→Vibrations，可以对各振动模式进行可视化，既可以观看动画，也可以用箭头标识出各原子的振动方向，如图5.2所示。

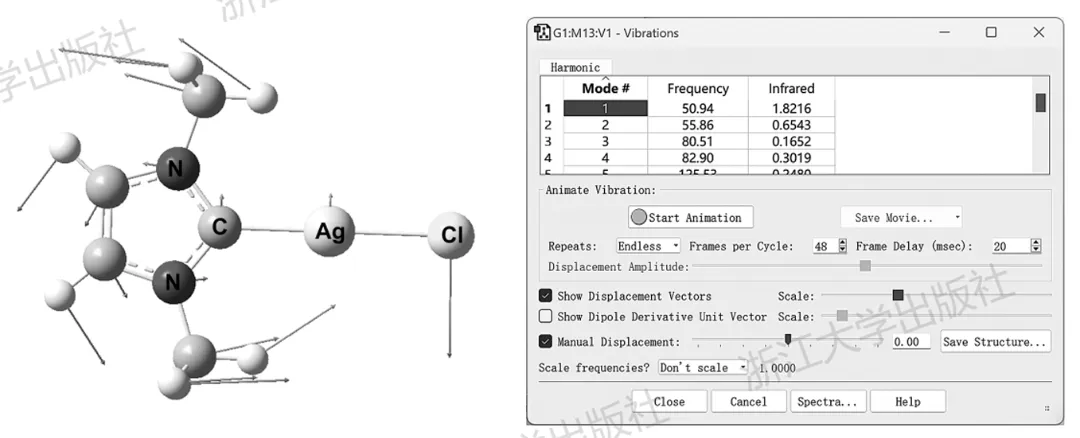
图5.2GaussView查看NHC-Ag配合物振动模式的可视化窗口

由此可以知道，这个频率为50.94cm⁻¹的振动模式对应于骨架的弯曲振动。用类似的方式，可以对各振动模式进行归属。点击Spectra按钮，可以显示红外光谱，其中各谱峰位置与振动波数一一对应，如图5.3所示。

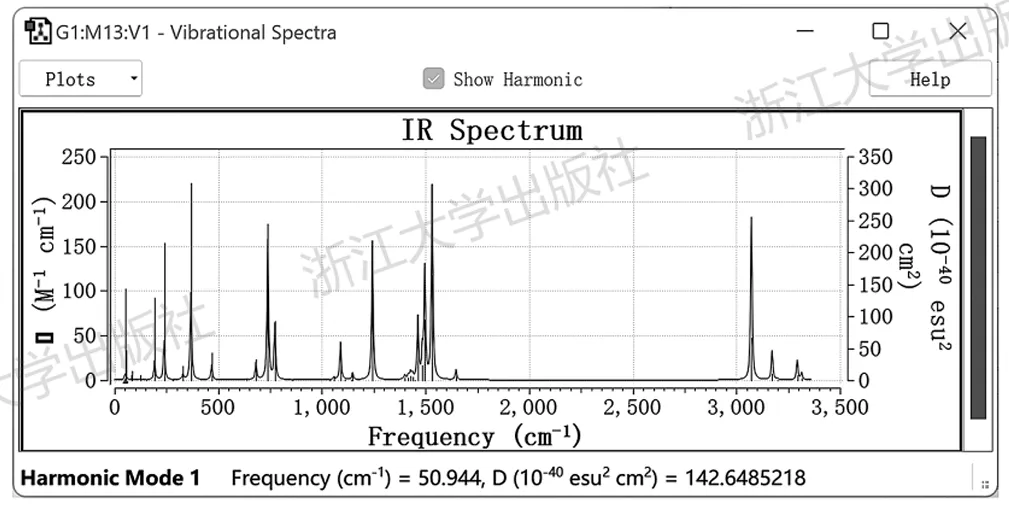
图5.3GaussView显示的NHC-Ag配合物的红外吸收谱图

拉曼光谱与红外光谱的原理相同而选律不同，使得分子偶极矩变化的振动模式表现出红外活性，而使得分子可极化性变化的振动模式表现出拉曼活性。如果想得到拉曼光谱，在频率计算时写上freq=raman关键字即可。

虽然使用Gaussian计算红外和拉曼光谱非常简单，但为了得到准确的红外光谱结果，还有一点提请注意：分子的非谐性。

在之前的讨论中，将各振动模式均认为服从谐振子模型。根据这一模型，随着偏离平衡位置的距离增大，能量以二次函数的形式上升至正无穷，而分子中显然不满足这一规律。随着结构偏离平衡位置，能量应逐渐过渡到平缓。这使得分子的能量-位置曲线呈现出如图5.4(b)所示的形状。

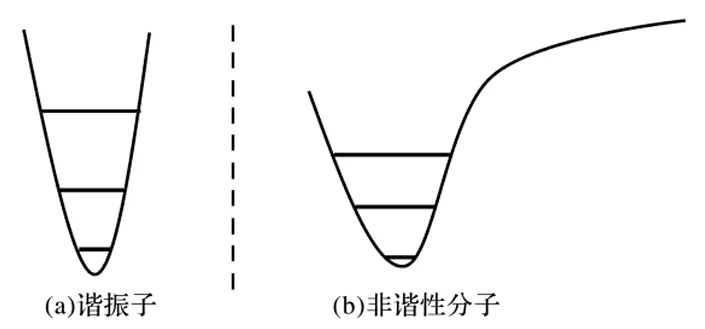
图5.4谐振子与非谐性分子的势能面和振动能级

能量曲线向平缓过渡带来的结果，可以看作是随着位置偏离平衡状态，能量曲线的“开口宽度”增加得比谐振子模型更快。而较大的开口宽度对应较小的力常数和较低的频率，因此真实分子的振动频率总是比谐振子模型下得到的振动频率低。也正是由于分子偏离谐振子模型的性质，导致真实测定出来的红外谱图非常复杂，峰的数目远多于计算得到的(对于非线性分子，如果有N个原子，则有3N-6个振动模式。显然，真实测定的红外光谱中峰的数量要更多)。

在量子化学计算中，虽然可以考虑非谐性进行频率计算，但耗时比普通频率计算高出若干个数量级，只能对于几个到十几个原子的小体系进行；并且许多情况下效果并不好。而幸运的是，经过大量实践，人们发现分子中某个振动模式的真实红外/拉曼吸收峰，与谐振子模型下计算得到的频率之间往往有很好的线性关系，只要在谐振子模型所得频率的基础上乘以一个系数，即可得到与测定值非常接近的频率。这个系数被称为基频校正因子。

基频校正因子与所使用的计算水平有关。绝大部分基频校正因子都落在0.9～1.0之间。对于大多数常用的计算水平，人们都已经拟合出了相应的基频校正因子。在http://bbs.keinsci.com/forum.php?mod=viewthread&tid=3805中，有人整理了各种来源的、大量计算水平下的基频校正因子。例如PBE0/6-31G(d)水平下的基频校正因子为0.9726，则直接将其乘以输出文件中每个振动模式的频率，即可得到与测定结果一致性很好的红外光谱(当然，非谐性导致的比3N-6个振动模式更多的谱峰仍然是无法得到的)。

借助Multiwfn程序的主功能11，基于频率计算的输出文件(log文件即可),也可以绘制红外或拉曼谱图。在这个过程中，可以输入校正因子，绘制出来的就是乘过校正因子的图形。与此同时，还可以调整展宽方式和大小。图5.5展示了上述NHC-Ag配合物用Multiwfn绘制出的红外谱图的效果。

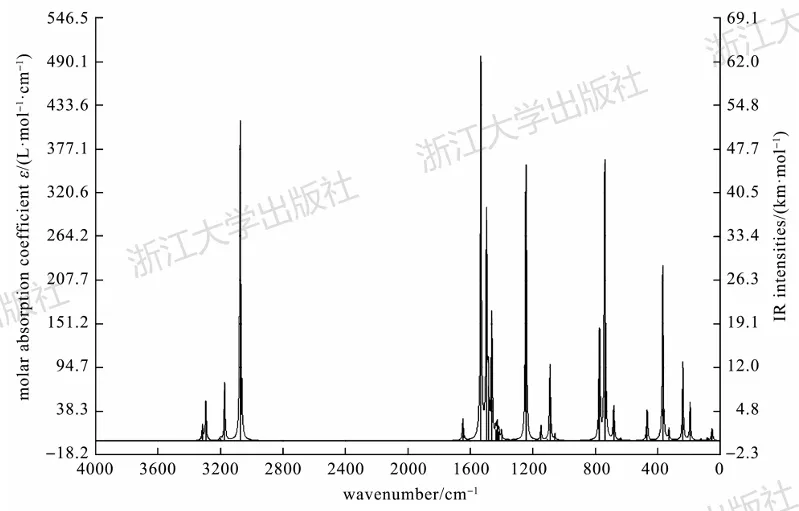
图5.5利用Multiwfn绘制的NHC-Ag配合物的红外吸收光谱

多位专家力荐  超全实战指南

↑扫码了解更多书籍及唯理计算信息