【摘要】 你这个精修结果能用吗?这是对数据精修处理之后的基本疑问,这些疑问本该在处理数据之前就有基本答案的。
拷问1:你这个精修结果能用吗?
三连1:Gof是什么,χ2是什么,R因子是什么?
这是对数据精修处理之后的基本疑问,这些疑问本该在处理数据之前就有基本答案的。
品质因子(R因子)用来判断文章中的精修结果是否可信,可信程度有多高。当然,需要注意的是,这些参数仅仅只是判断“拟合”的质量,更为重要的是,考虑结构的化学合理性[1]。
一、精修的数学方法是什么?
1.1 简单线性最小二乘
在考虑复杂的晶体结构最小二乘精修之前,我们使用一个简单的具有两个系数的一次函数y = kx +b来说明最小二乘法。
A、当只有两个观察点(x1,y1),(x2,y2)的时候,我们有两个未知数,两个方程:
y1 = k*x1 + b
y2 = k*x2 + b
矩阵形式如下:
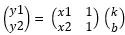
此时:
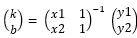
B、当只有十个个观察点(x1,y1),(x2,y2)…(x10,y10)时,我们有两个未知数,十个方程:
y1 = k*x1 + b
y2 = k*x2 + b
…
y10 = k*x10 + b
矩阵形式如下:
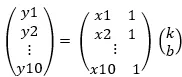
此时,k和b的解析数值可由任意两个方程确定,但该数值决定于选取的方程组,因此k和b不是唯一的。此时,我们就有一个疑问,什么样的k和b才是最优解。为此,我们定义最优k和b满足(yi - ycalc)^2值最小,在我们线性函数的描述中,定义函数
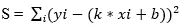
当S值极小时,需满足如下条件:
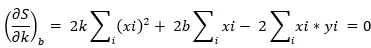
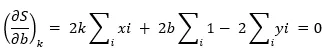
由此得到“最优的”k值和b值。

1.2 非线性最小二乘
常见的衍射数据横轴为2theta,纵轴为强度值,间隔步长的每个数据点对应一个强度值,即:(xi, yi);我们将测试的一组数据记为(xo,i, yo,i),模型计算的一组数据记为(xc,i, yc,i),精修过程即通过优化各种参数将计算值与观测值的加权方差值达到最小,即:
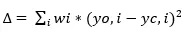
达到最小值。
和线性最小二乘法类似,对于不同的参数pj,该函数取得“最小值”的条件如下:
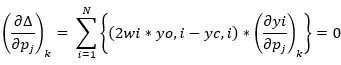
其中,N为所有的观测数目。如果有M个参数,则有M个方程。现假设我们有一个接近满足以上方程的晶体结构模型,但是模型参数与真实的“最小值”有一个小的差异“”。应用泰勒级数展开:
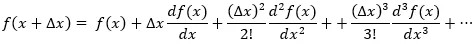
当∆x接近于δx→0时,高阶项(n > 1)可以忽略。
这也是非线性最小二乘精修的基础。应用泰勒级数展开:
…
中间省略,又长又麻烦,不想写,有兴趣的自己去查询
…
二、R因子都有哪些?
R因子大家可能都有所了解。如下表1所示[2],列出来粉末衍射精修中涉及到的R因子。那我们如何才可以找到我们所要的数值并正确将他们区分开来,关于粉末衍射精修中常见的R因子有以下三种:

Rp,R-pattern,中文名为图形方差因子;Rwp,R-weighted pattern,中文名为加权图形方差因子,二者都是对拟合图形的描述。
Rexp,R-expected,中文为期望方差因子。很多人在问,Rp或者Rwp到什么水平是可以用的,在有这个疑问之前,首先要对自己的数据有一个量化认识,以下使用MATLAB对同一半高宽的高斯峰进行拟合,并给出拟合的Rp结果。
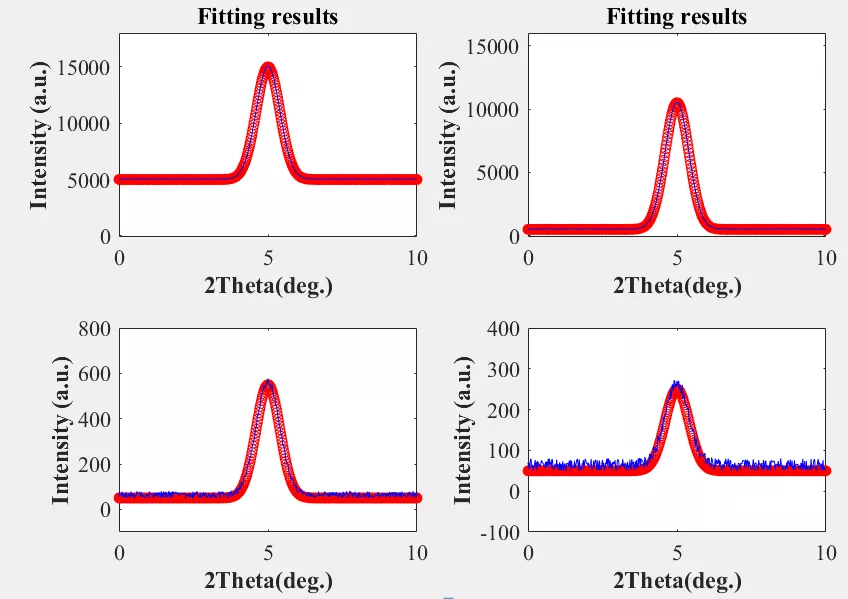
|
A:Rp = 0.0065 |
B:Rp = 0.0269 |
|
C:Rp = 0.1448 |
D:Rp = 0.2061 |
-
A图的Rp = 0.0065,即:0.56%,这是一个很低的数值。这是因为衍射峰的计数强度有很明显的一部分是来源于背地,Rp计算式的分母项很大,自然得到的Rp就会小。很多同学在精修具有荧光背地的数据,比如:含有过渡金属元素的样品或者其他背地计数很高的数据,很容易获得很低的R值,这时候就不能用所谓的R值在12%以内之类的绝对数值来说明精修的质量了,背地带来的统计已经对R因子有很强的影响了;
-
B图为同样相对强度的数据,但是背地的计数不高,此时的Rp = 0.0269,即:2.69%,这是一个看起来很舒服的数值;
-
C图中的该峰强度计数为604,背地平均计数为40,背地的sigma约为40,此时信噪比较低,计算所得的Rp为14.5%,是一个在“不可用”边缘来回试探的数值;
-
D 图中的该峰强度计数为286,背地平均计数为40,背地的sigma约为40,此时信噪比很低,计算所得的Rp为20.61%,显然的,Rp的分子式小,因此计算得到的Rp数值就会大,这个数值审稿人看起来不是很喜欢。
除了以上三种R因子外,还有两类R因子也值得我们考虑。其一为Rf,为结构振幅剩余方差因子(该叫法来源于参考文献2),表示布拉格衍射的结构振幅的观察值与计算值之间的差异;另一个为Rb,为布拉格方差因子,表示布拉格衍射积分强度的观察值与计算值之间的差异。在只修正图形参数的过程中,这两个R因子是没有被应用的,但是当对结构参数进行修正后,这两个R因子也会自然的降低。
只要知道R因子的表达式,结合自己的数据,自然就能知道什么样的数据能获得什么样子的R因子结果。
三、如何使用R因子?
3.1 数形结合
R因子是数学上的参考判据,它仅仅是一种数学统计处理手段。在合理使用R因子的基础
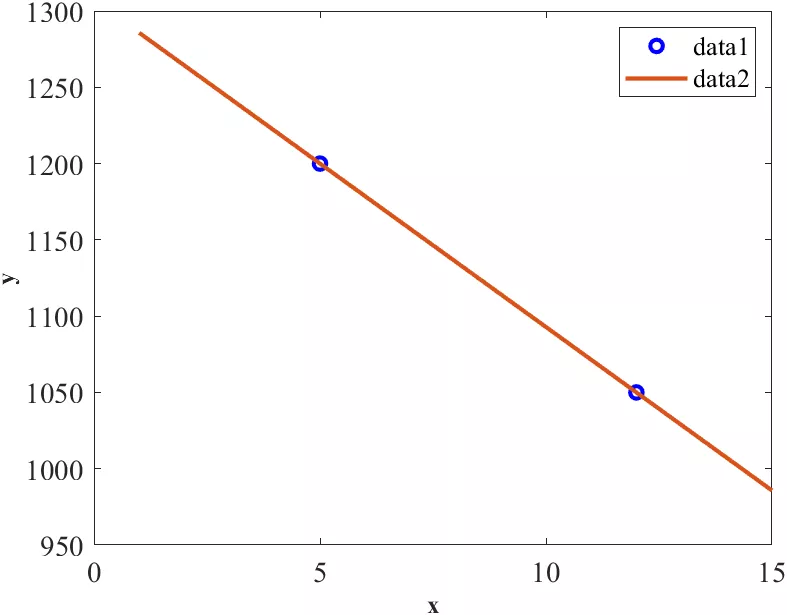
上,我们可以将它与图形结合起来,形成一个“数形结合”的判断依据。“数”即R因子,这个已经在上文提到,而所谓“形”即:图形,图谱。在粉末衍射中我们需要重点关注的为“差值线”,如下图中的蓝色的“Diff”线,这个线越平直,表明精修强度值与实际测试强度值差别越小,二者越接近。
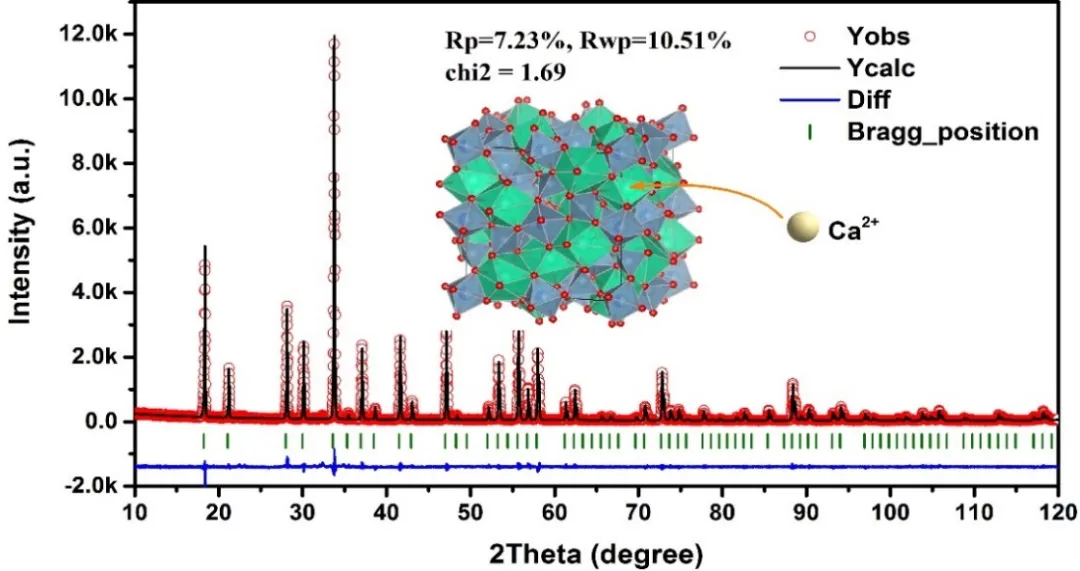
如上图所示,可观察蓝色差值线比较平,没有特别明显的“波澜壮阔”的情况,同时其χ2 =1.69,小于2,二者结果对应,表明该精修结果满意。
3.2 综合考虑
(1)对于质量较好的数据,Rwp应该小于0.12(参考数值);
Gof(S)应该小于2,但是不能低于1;
不建议单独使用R因子或者单独使用Gof。对于高噪声的数据Gof很容易降为1左右,对于超高强度、低噪声的数据,R因子很容易达到0.12左右。
(2)可精修的参数需收敛,符合化学结构合理性。比如,键长键角的合理性,元素组分及电价的合理性。
(3)不能一概而论,以上部分已经说明R因子及S与原始数据联系紧密,因此,要结合自己的数据来判断精修结果。比较合适的处理方法就是收集一个满足要求的原始数据去精修,好的数据是成功的一大半。在收集数据的时候,注意步长、计数、样品制备等条件,尽可能消除折优,样品不平等对数据带来的影响。
没有高质量的数据,就不要轻易问精修结果是否可用。
四、Fullprof中的R因子
使用Fullprof精修完成后,可以在Sum、Out、CIF(如果勾选)文件中查看相应的R因子。这里以Sum文件为例,使用记事本打开,找到如下的语句:
“RELIABILITY FACTORS WITH ALL NON-EXCLUDED POINTS FOR PATTERN”
“Reliability factors with all non-excluded points for pattern”
…
例如:
==> RELIABILITY FACTORS WITH ALL NON-EXCLUDED POINTS FOR PATTERN: 1
=> Cycle: 12 => MaxCycle:100
=> N-P+C: 3420
=> R-factors (not corrected for background) for Pattern: 1
=> Rp: 6.24 Rwp: 8.60 Rexp: 5.87 Chi2: 2.15 L.S. refinement
=> Conventional Rietveld R-factors for Pattern: 1
=> Rp: 19.1 Rwp: 16.2 Rexp: 11.04 Chi2: 2.15
可以看出,有两类R因子,第一类为“R-factors (not corrected for background)”;第二类为“Conventional Rietveld R-factors”,从字面意思可看出,第一类R因子为不矫正背地时获得的R因子,该R因子为原始数据对应的R因子,首选该R因子:即该数据的Rp=6.24%,Rwp= 8.60%,Rexp=5.87%,Chi2= 2.15,这里的Rexp是取决于原始数据的。第二类R因子为传统的R因子,与第一类的区别在于使用的是背地矫正后的计数。
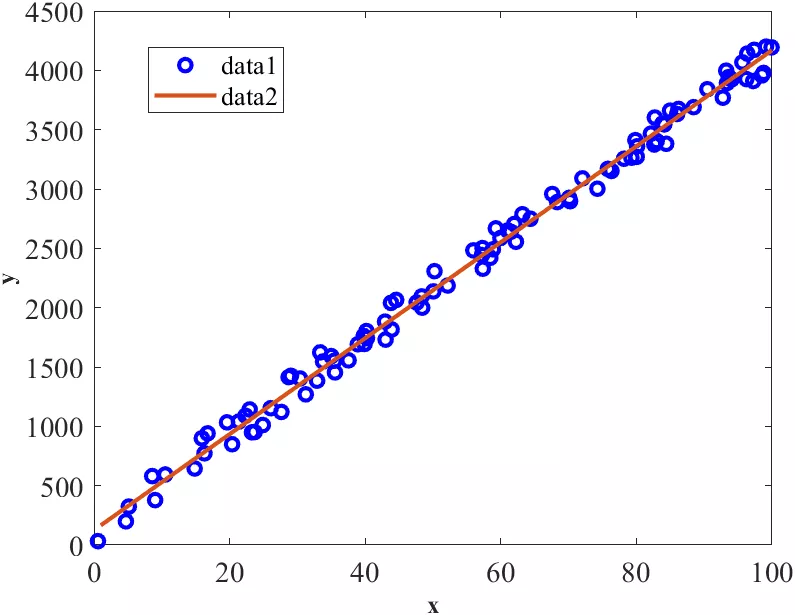
为了说明该情况,对如下两组数据进行精修处理:
数据说明:
两组数据只是在背地绝对计数值上有差别,衍射峰的相对强度值一致,即:数据2只是在数据1的基础上同时+2000;
精修结果:
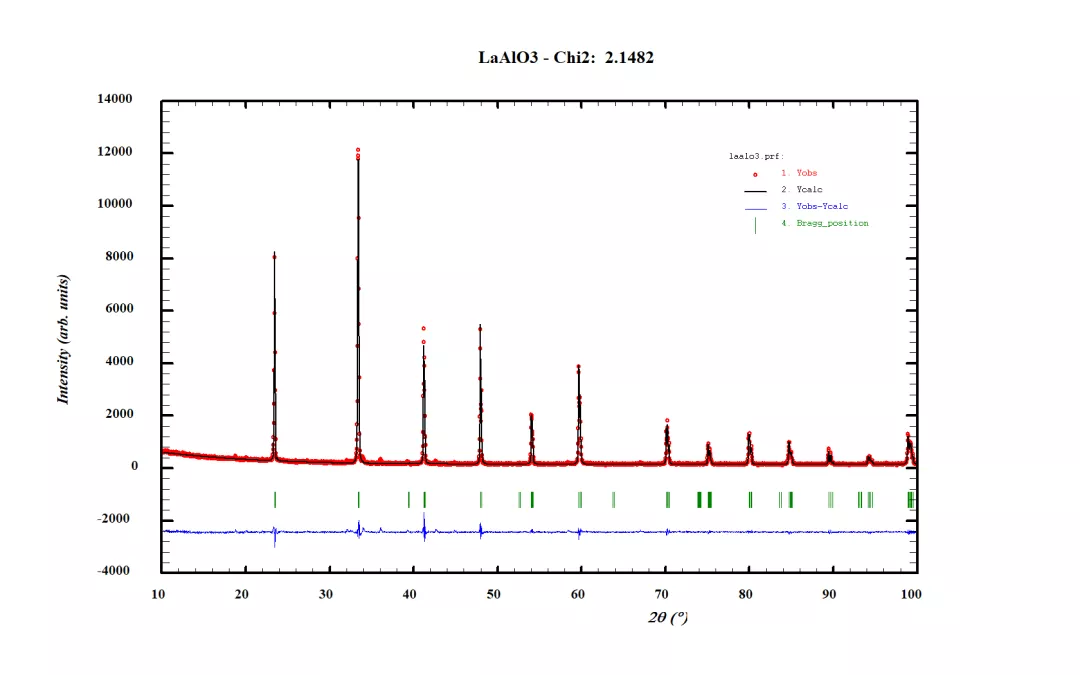
=> R-factors (not corrected for background) for Pattern: 1
=> Rp: 6.24 Rwp: 8.60 Rexp: 5.87 Chi2: 2.15 L.S. refinement
=> Conventional Rietveld R-factors for Pattern: 1
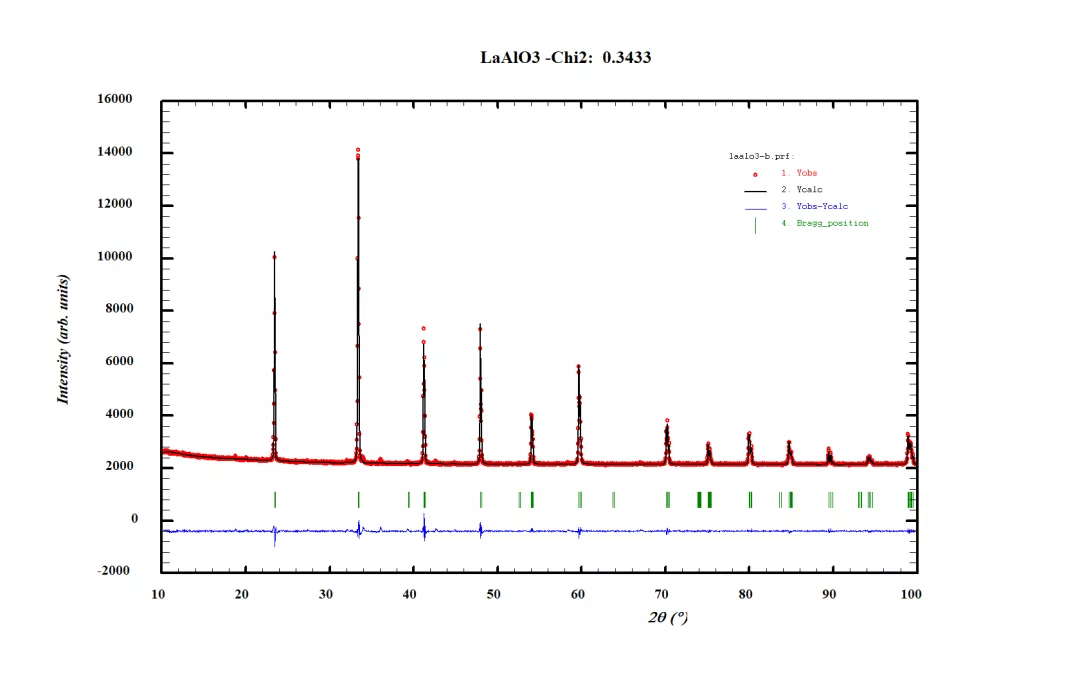
=> R-factors (not corrected for background) for Pattern: 1
=> Rp: 0.762 Rwp: 1.21 Rexp: 2.07 Chi2: 0.343 L.S. refinement
=> Conventional Rietveld R-factors for Pattern: 1
仅仅只是对整个原始数据1进行y方向平移,给出的Rexp及Chi2的数值差别如此明显,但是这两个精修所得的结构是一致的。自行体会。
参考文献
[1] Toby B H. R factors in Rietveld analysis: How good is good enough?[J]. Powder diffraction, 2006, 21(1): 67-70.
[2] 梁敬魁. 粉末衍射法测定晶体结构. 下册[M]. 科学出版社, 2011.
小编学识有限,错误之处请批评指正。
以上文章来源于XRD Refinement ,作者王小z











 您已经拒绝加入团体
您已经拒绝加入团体

 2022-02-22
2022-02-22
 15521
15521
 0
0










