【摘要】 密度泛函理论(Density Functional Theory),简称DFT。它包含了两种理解,一种是由Kohn等人提出的量子方法,用于解释非均相基态的电子结构;另一种是由Ebner等人提出的经典方法,用于研究Lennard-Jones流体的界面性质。
(2)密度泛函理论
密度泛函理论(Density Functional Theory),简称DFT。它包含了两种理解,一种是由Kohn等人提出的量子方法,用于解释非均相基态的电子结构;另一种是由Ebner等人提出的经典方法,用于研究Lennard-Jones流体的界面性质。本研究讨论的是经典密度泛函理论。
经典密度泛函理论的关键在于构建基于粒子密度的Helmholtz自由能函数,而此函数是在界面自由能函数最小化的基础上构造的。一般来说,Helmholtz自由能分为两部分:一部分是只包含理想相互作用和短程相互作用的参考项,另一部分是包含长程相互作用的扰动项。其中,参考项可以用局部密度近似(LDA)或加权密度近似(WDA)来处理。而一旦知道了平衡密度分布,就可以确定界面张力。其最终计算公式如方程(4)所示。
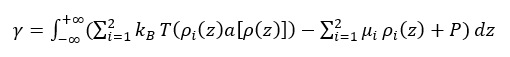 (4)
(4)
式中,γ为界面张力;kB为玻尔兹曼常数;T为温度;Pi(z)是第i个分量在z处的局部数密度; 为每一组分的主体化学势;Р为平衡时的压力。
经典密度泛函理论用于计算界面张力时结果精确。但由于其理论较为复杂,计算时需要的分子间作用参数较多,因此限制了该理论的发展。
(3) 密度梯度理论
密度梯度理论是一种较为严格的理论计算方法。该方法由van der Waals提出,其核心是认为非均相流体的Helmholtz能量密度沿界面的变化是连续的,由此可以计算出非均相流体的界面性质。后来,该理论由Cahn和 Hilliard进行了改良,可用于多种体系界面张力的计算。根据该理论,界面的Helmholtz自由能密度为均相部分和非均相部分的加和,Helmholtz自由能密度可由Taylor二阶展开式表示,如方程(5)所示。
 (5)
(5)
式中,F为Helmholtz自由能,J;f(ρ1(r),ρ2(r))为均相流体的Helmholtz自由能密度,J/m3;ρ1(r),ρ2(r)为摩尔密度,mol/m3; cij为影响因子,J•m5/mol;![]() 为局部密度梯度。
为局部密度梯度。
[1] Hohenberg P, Kohn W. The inhomogeneous electron gas [J]. Physical Review B,1964,136(3):864-871.
[2] Ebner C, Saam W F, Stroud D. Density-functional theory of simple classical fluids. I. surfaces [J].Physical Review A, 1976,14(6): 2264-2273.
[3] Tang X,Gross J. Density functional theory for calculating surface tensions with a simple renormalization formalism for the critical pointJ]. Joumal ofSupercritical Fluids,2010,55(2): 735-742.
[4]李琳.CO_2驱油技术中CO_2-烃类体系界面张力的研究[D].天津大学,2020.
免责声明:部分文章整合自网络,因内容庞杂无法联系到全部作者,如有侵权,请联系删除,我们会在第一时间予以答复,万分感谢。











 您已经拒绝加入团体
您已经拒绝加入团体

 2022-04-21
2022-04-21
 9788
9788
 0
0










