【摘要】 界面张力可以看成是作用在单位长度液体界面上的收缩力，在数值上与比界面能相等。

在平衡状态下，界面上的密度分布满足下面的Euler-Lagrange方程:

 

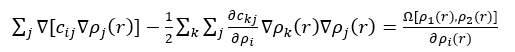（6）

 

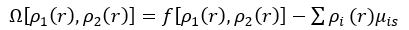其中，（7）

 

式中，为体系的巨势密度；为状态方程计算出的组分i的相平衡化学势。

 

由于仅在界面的法向(z方向）上存在密度梯度，且影响因子对密度的变化不敏感，因此可忽略密度对影响因子的作用，方程（6）可简化为:

 

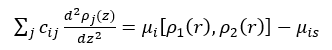（8）

 

将方程（7)的两边同时乘以，并求和积分得到方程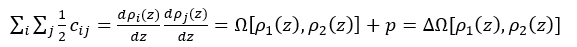（9):

 

（9）

 

式中，P为平衡时的压力,Pa。

 

由此得到出界面张力的表达式为:

 

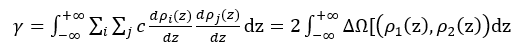(10)

 

其中，对于二元混合物，若将组分2作为参考流体，消掉空间变量z，混合物的二元影响因子c及界面层组元密度导数dp1(z)/dp2(z)的表达式如方程(11)、(12)所示。

 

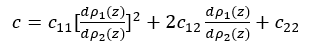(11)

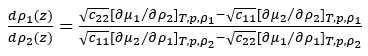(12)

 

(4)线性梯度理论

线性梯度理论是由Zuo和Stanby等人在密度梯度理论的基础上提出的。该理论假设:混合物中各组分的密度在液-汽界面上呈线性分布。因此，该方法下组分i在相界面z处的密度可表示为:

 

 

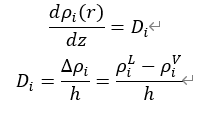
式中，其中Di为常数; 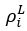和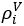分别为边界条件下组分i的液相密度和汽相密度。

由此可得到界面层组元密度导数dp1(r)/dp2(r)的表达式（将组分2作为参考流体)，如方程（13）所示:

 

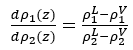（13）

 

由于线性梯度理论是在密度梯度理论的基础上发展而来,因此其界面张力的表达式与密度梯度理论类似。

 

线性梯度理论简化了对密度分布的计算，与形式简单的立方型状态方程结合可广泛应用于多种体系界面张力的计算。

 

[1] Zuo Y x, Stenby E H.A linear gradient theory model for calculating interfacial tensions of mixtures [J].Journal of Colloid & Interface Science，1996,182(1):126-132.

[2] Zuo Y X, Stenby E H. Calculation of interfacial tensions with gradient theory[J].Fluid Phase Equilibria,1997,132(1-2):139-158.

[3]李琳.CO_2驱油技术中CO_2-烃类体系界面张力的研究[D].天津大学,2020.

 

免责声明：部分文章整合自网络，因内容庞杂无法联系到全部作者，如有侵权，请联系删除，我们会在第一时间予以答复，万分感谢。