【摘要】 在主磁滞回线和初始磁化条件下，该模型的实现精度较高。

也许最重要和最常用的构造迟滞回线和反转曲线的方法是由Preisach提出的。这种方法也被称为经典的Preisach模型，已被许多作者广泛用于表示各种磁化过程。另一种与磁化动力学物理机制相关的重要方法称为Jiles - Atherton模型，它通过微分方程描述输出变量。在过去的30年里，除了这两个模型之外，还提出了许多其他模型。研究人员已经使用了各种方法和技术来模拟材料中的磁滞回线和磁化瞬态。

 

ALENKA等人[1]提出的模型是基于正切反函数的。该函数用于主磁滞回线和初始磁化曲线的建模。一个简单的程序已被用于构造一阶反转曲线(FORCs)。通过复制构建的forc的特定部分，可以获得二阶和高阶曲线，考虑到消去和同余属性。这为模型提供了非局部内存行为。在主磁滞回线和初始磁化条件下，该模型的实现精度较高。用其所提出的模型计算了各种形状的迟滞回路，包括对称和非对称小回路和瞬态轨迹，以证明其适用性。将得到的结果与测量和模拟得到的结果进行了比较，发现所有结果之间的一致性非常好。

图1. 测量和模拟了主要的磁滞回线[1]

 

模拟主回路的精度可以通过计算其面积来检验。图1所示模拟主回路的计算面积为194.46，而实测主回路的面积为247.418。这两个结果的相对偏差为-21.4%。修正后，模拟主回路(图1)的面积增大，为230.412。结果之间的新相对偏差为-6.87%。通过稍微修改模型参数，可以进一步改善结果。如果将下降曲线的下一个模型参数设为a = 1.025, b = 0.0992, c = 0.0002636，上升曲线(正部分)设为a1 = 1.02, b1 = 0.0527, c1 = 0.0003136，则图2中模拟回路的面积为242.22，两者之间的相对偏差为-2.1%。仿真结果的精度在实际应用中是可以接受的。

 

总之，ALENKA等人提出了一种新的主磁滞回线模型。该模型有四个参数，可以从测量的主回路确定。这些参数的计算采用了简单的表达式。这些表达式将给出模型参数的初始值，应该稍微调整以适应被测量的回路。此外，已经证明主回路不是完全对称的。因此，将主回路的上升和下降部分表示为具有不同模型参数值的两件式函数。为此，引入了“虚构剩余归纳法”一词。 

 

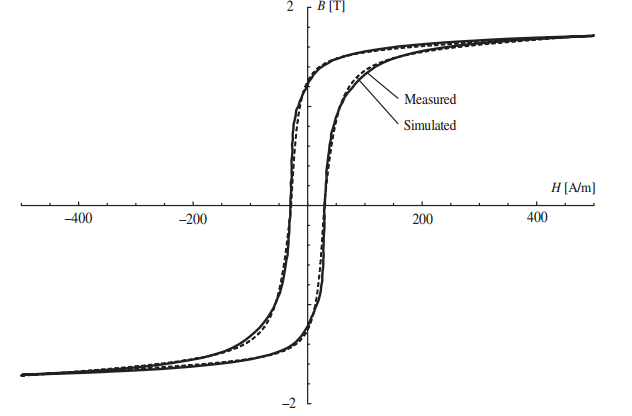
图2.测量和模拟了主要的磁滞回线[1]

 

[1] Milovanovic, Alenka M.; Koprivica, Branko M. (2015). Mathematical Model of Major Hysteresis Loop and Transient Magnetizations. Electromagnetics, 35(3), 155–166. 

 

科学指南针已获得检验检测机构资质认定证书（CMA）、实验动物使用许可证、“ISO三体系认证”等专业认证，并荣获国家高新技术企业、国家“互联网+科研服务领军企业等多项荣誉。未来，科学指南针将继续朝着“世界级科研服务机构”的目标，在产品研发和用户服务等方面持续努力，为科学发展和技术创新做出更大贡献。

 

免责声明：部分文章整合自网络，因内容庞杂无法联系到全部作者，如有侵权，请联系删除，我们会在第一时间予以答复，万分感谢。