非线性光学晶体双折射的贝德电荷积分原子分辨分析

Vidal-Valat(1975)在室温下对MgF进行了x射线衍射研究，得到了晶格参数:a =b=4.628 (5)， c= 3.045 (3) a, x= 0-303对应d= 1-981 (2) a。用Kurki-Suonio(1967)方法进行的直接原子电荷密度分析表明，氟向镁转移了一些电荷。

然而，原子变形的影响和位置移动的影响是无法区分的。此外，观测到的各向异性明显包括热运动和变形的贡献，这两个因素不容易相互分离。解释的困难部分是由消光效应引起的，在x射线实验中清楚地观察到消光效应的存在。给出了一个用这种原子分辨分析方法计算MgF₂晶体的例子。

DFT计算采用实验晶体结构(金红石型)，晶格常数a = b = 4.615 Å， c = 3.043 Å，空间群号为136(图1)。利用Perdew-Burke-Ernzerhof (PBE)给出的交换相关性与广义梯度近似(GGA)。

价电子是Mg 2s² 2p⁶ 3s²和F 2s² 2p⁵。设置平面波截止能量为900eV。自一致收敛容差设置为1.0 x 10^-6 eV/原子。Monkhorst-Pack采样的k点网格设置为5 × 5 × 8，对应于每个晶体轴为0.04 Å ^-1。空带数设为150，是总价电子数的3倍。MgF₂的能带结构如图2所示。计算带隙为7.287 eV，实验带隙为10.8或12.4 eV。

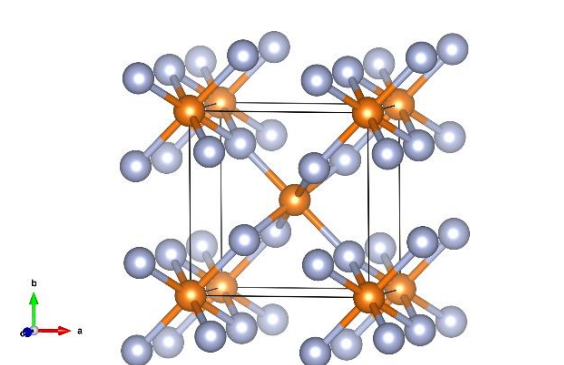
图1 MgF₂的晶体结构。

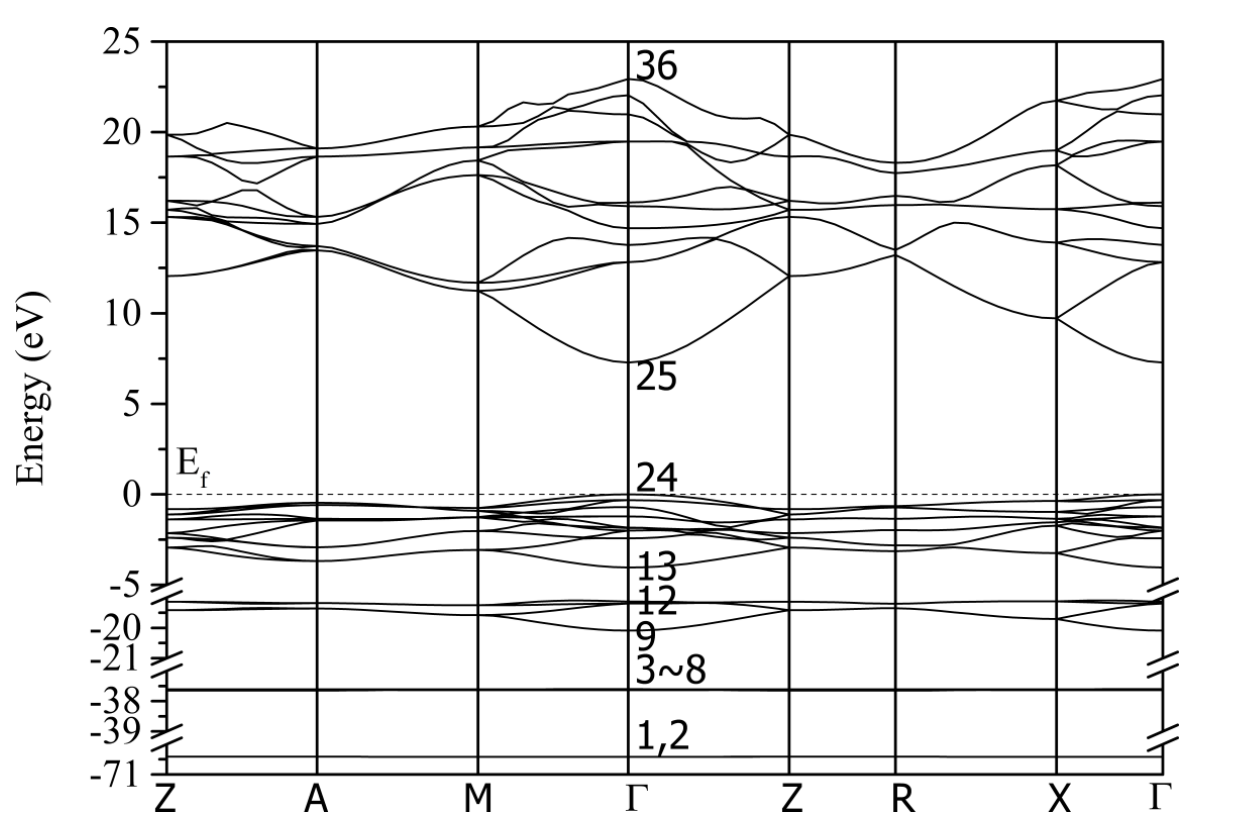
图2 MgF₂的能带结构。

Lin等人¹用带隙10.8 eV作为实验值。因此，在下面的光学性质计算中，剪刀算子设为3.513 eV。GGA计算得到的介电常数虚数如图3所示。

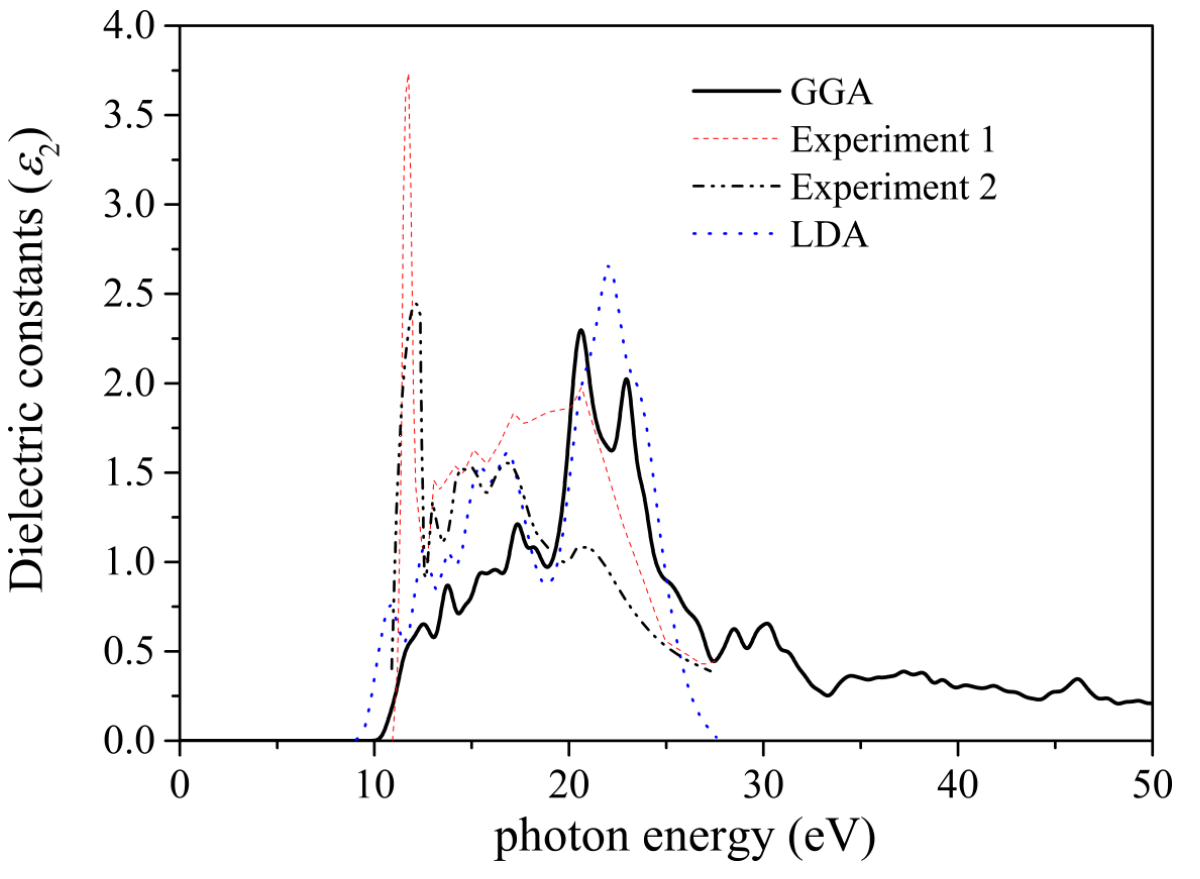
图3 MgF₂介电常数的虚部。

与文献LDA计算结果一致然而，GGA和LDA计算的介电常数都不如实验结果密集。这可能是由于在DFT计算中使用的交换相关模型的不足。

因此，计算出的折射率略小于实验观测值。在入射光子能量为1.164 eV时，根据测量数据推导出的Sellmeier方程，计算得到的n_a和n_c分别为1.3450和1.3573，而实验数据为n_a = 1.3727和n_c = 1.3843。

然而，在c轴和a轴方向上，计算出的介电常数都被低估了。因此，在入射光子能量为1.164 eV时，GGA计算得到的双折射(n_c - n_a)值为0.0123，与实验得到的双折射值0.0115吻合较好。应用文中描述的方法，沿c轴和a轴各波段对介电常数的贡献。使用Bader分析(表1)，该研究最终得到MgF₂双折射的原子贡献为Mg: 18%和F: 82%。

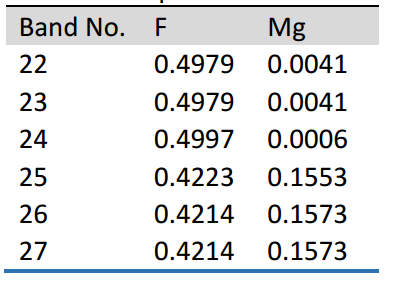
表1 一些价带和导带在k点的原子贝德有效电荷(e)

1.Lin, c.;  Zhou, A.-y.;  Cheng, W.;  Ye, N.; Chai, G., Atom-Resolved Analysis of Birefringence of Nonlinear Optical Crystals by Bader Charge Integration. The Journal of Physical Chemistry C 2019, XXXX.

科学指南针充分发挥互联网技术和业务优势，在国内率先打造出业界领先的线上化、数字化的科研服务基础设施，在行业内首创用户自主下单、服务全流程追踪、测试“云现场”等模式，进一步提高了大型科学仪器设施开放共享和使用效率，以实际行动助力科技创新。现已发展成为中国专业科研服务引领者，已获得检验检测机构资质认定证书（CMA）、实验动物使用许可证、“ISO三体系认证”等专业认证。

免责声明：部分文章整合自网络，因内容庞杂无法联系到全部作者，如有侵权，请联系删除，我们会在第一时间予以答复，万分感谢。