【摘要】 已经发现电化学中有许多场合很难得到电流、电势和时间之间的显式关系式。

已经发现电化学中有许多场合很难得到电流、电势和时间之间的显式关系式。这不是因为体系本身内在复杂(例如, 涉及反应物质吸附和扩散的准可逆电荷转移) , 就是因为实验条件不理想(例如, 阶跃实验是在足够短的时间域上完成的, 致使恒电势仪的上升时间不可忽略)。通常情况确实如此, 但也有些场合在扰动和观察值之间, 在Laplace 域中存在着比较简单的关系。因此, 在变换空间进行数据的变换和分析可能是有益的。

作为一个例子, 来讨论对含有能准可逆还原的、单步骤单电子电活性物质O 的体系上施加电势阶跃的情况。

其电流-时间函数为

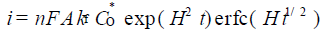            1.1

其中，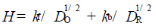

体现在式(1.1) 中的复杂的时间关系, 对于实际数据的分析

是困难的。因此, 设计了线性化或外推等各种办法。另一方面, 通过采用变换的电流, 可以使用所有数据而无需引进这样的近似值:

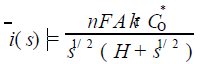                                                1.2

例如, 可以将函数1/ i( s ) s1/ 2 对s1/ 2 作图。从所得线性函数的斜率和截距可给出kf 和H。在进行此

项工作时, 我们是选择在s域而不是在时间域中分析体系。

为了实现这一目标, 必须从测出的曲线i( t) 得到函数i( s)。这可以通过Laplace 变换的定义来完成

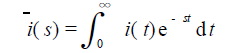                                           1.3

在实际情况下, i( t) 通常是数据点的集合。因此, 对于给定的s 值, i( s) 是通过把每一个点乘以e- st 然后将所得曲线进行数值积分计算出来的。对每一个所求的s 值重复整个过程, 最后结果是表示i( s) 的数据点的新的集合, 正如原始数据表示i( t)一样。因为s 具有频率的量纲, 有时称i( s) 为电流在频率域中的表达式。

下一期我们继续讲解。

参考文献

《电化学方法原理和应用》第二版_美_阿伦.J.巴德_等著

 

科学指南针通过互联网技术建立更可靠的服务标准，全国26个办事处，12个城市拥有自营实验室，最好的设备、最专业的老师为您服务。

 

免责声明：部分文章整合自网络，因内容庞杂无法联系到全部作者，如有侵权，请联系删除，我们会在第一时间予以答复，万分感谢。