分子模拟-定量分子模拟

原则上，量子力学准确地描述了任何尺寸的化学体系的能量学。然而，尽管可利用的计算能力不断增加，确定大型系统遵循其分子动力学所需的相互作用和力量在计算上却变得难以实现。这是由于电子数目和准确求解薛定谔方程所需的大量基函数不利于电子结构计算的缩放，尽管线性缩放方法为这些缺点提供了一些补救措施。对核自由度的量子力学处理甚至更加需要计算，典型的系统大小为10个重原子，严格的计算是可行的。

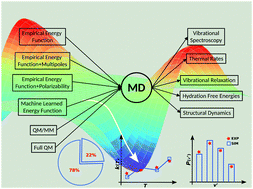
图1分子模拟领域

另一方面，经验分子力学(MM)能量函数(“力场”)在计算上有利于评估。传播基于牛顿运动方程的动力学可以获得大分子系统的长时间尺度。在这种情况下，“长时间尺度”是亚微秒级的，“大系统”意味着109个原子，其性能可达到8ns-1天。这种分子动力学(MD)模拟已被用于研究从蛋白质折叠，配体结合在细胞环境中的拥挤到表征溶质和肽的光谱特性以及在气相和溶液中的反应的过程。

然而，其中一个挑战仍然是开发合适的能量函数，以保持它们经常基于的量子计量方法的精确度，并且适合于遵循键断裂和键形成。

一维或多维振动光谱是表征复杂系统结构动力学的有力手段。实验大大有益，通常需要伴随分子水平解释的MD模拟。这样的原子模拟依赖于键合和非键合的相互作用，以一种有意义的方式来描述这种相互作用，从而与实验直接接触。

传统上，经验能量函数使用化学键和价角的谐波弹簧，二面体的周期函数，基于原子中心的点电荷模型，范德瓦尔斯相互作用的Lennard-Jones表示，以及其他更加量身定制的项。对于光谱学的应用，化学键(拉伸振动)需要更加现实地描述，以说明机械不谐波，其中摩尔斯振荡器往往是足够的，因为在环境温度下的实验对高度振动激发态不敏感。

尽管如此，仍有余地使用更精确的表示，例如基于机器学习类型的方法，特别是如果有来自高级电子结构计算的参考数据。对于非粘结相互作用(包括静电和范德瓦尔斯术语)，已经开发了更多超越标准表示的基于物理的模型。

静电相互作用的一级处理是基于库仑相互作用的原子中心点电荷。这样的对相互作用可以快速计算，但是缺乏描述各向异性对电荷密度贡献的准确性。包括高阶原子多极提高了准确性，但是计算成本和实现复杂性增加了。考虑极化性是另一个贡献，最近已经包括在经验力场中，并显示出进一步改进计算模型的很大希望。从经验力场的角度来看，范德瓦尔斯相互作用通常表示为Lennard-Jones术语与特别(Lorentz-Berthelot)组合规则。替代和潜在改进的表示是缓冲的参数化和修改后的组合规则。

目前研究气相和凝聚相中反应系统的方法包括混合量子力学/分子力学(QM/MM)，反应力场ReaxFF31和反应分子动力学(RMD)。反应力场的一般方法是用一个单独的能量函数描述反应物和产物的状态，并通过混合函数或对角化n×n矩阵来连接这两个状态，其中n是所考虑的状态数。这个反应部分被嵌入到一个环境中，这个环境被一个更经验的能量函数描述，类似于混合的QM/MM计算和模拟。

近年来，各种复杂的机器学习(ML)潜力被开发出来，以准确地表示高水平参考计算的从头计算结果(见参考文献。及其中的参考文献)。这种基于ML的能量函数也扩展到气相中的反应系统，用于解决方案和表面上的模拟，最近还提出了用于气相中的复合系统以研究复杂的燃烧过程、

从技术角度来看，表面反应的计算研究特别有意义。多相催化反应在化学工业中有着广泛的应用，是一个重要的经济因素。理论和实验研究的重点不仅在于化学键的形成和断裂，而且在于扩散过程以及散射实验的预测。考虑的体系包括金属、金属氧化物、矿物或离子化合物的单晶表面到石墨烯片、无定形多孔碳和水表面。它们可以通过吸附在金属载体上的超薄层、使用金属合金或通过金属团簇或单个原子或空位的纳米结构来修饰。特别相关的是具有配位的表面位置——表面边缘的不饱和原子、扭结或空位已被发现是反应性增强的位置。然而，用高能电子量子方法中的杂质建立这种表面的模型仍然是一项具有挑战性的任务，特别是如果寻找动力学信息的话。

将具有量子力学处理精度的方法与计算性能相当于经验力场的方法相结合，将为在定量水平上研究反应过程和光谱特性开辟可能性。2013年诺贝尔化学奖承认了这方面的进展。然而，应用精确的，基于物理学的力场进行凝聚相模拟仍然不是常规。目前的工作着重介绍了我们自己的工作和实地同事的具体应用，展示了这种方法的机会，并讨论了今后的前景和在更广泛的意义上减缓更迅速地适应这种方法的原因。这个定量MD模拟领域的概述侧重于物理化学和生物物理中出现的问题的应用。在目前的情况下，定量方面的判断是通过比较现有的实验数据。因此，系统的实验和计算角色塑造之间的密切关系是必不可少的。

1.Töpfer K, Upadhyay M, Meuwly M. Quantitative molecular simulations[J]. Physical Chemistry Chemical Physics, 2022, 24(21): 12767-12786.