【摘要】 小编今天简单介绍一些统计学中常见参数检验和非参数检验问题的解决方法及适合应用的情况。

小编今天简单介绍一些统计分析中常见参数检验和非参数检验问题的解决方法及适合应用的情况。

 

单样本t检验

 

单样本t 检验，用于研究样本的均数与总体均数是否相等，适用于样本平均数来自正态分布总体的情况；

 

成组t检验

 

成组t 检验，也被称为两独立样本资料的t检验，适用于完全随机设计的两样本均数的比较。

 

除了要求数据独立，还要求两组数据所代表的整体服从正态分布且整体的方差相等，即方差齐性。

 

如果不服从正态分布，则需要对数据进行变换或使用非参数检验；如果方差不齐，则需要对数据进行校正、变量转换或非参数检验。效果如图1所示

 

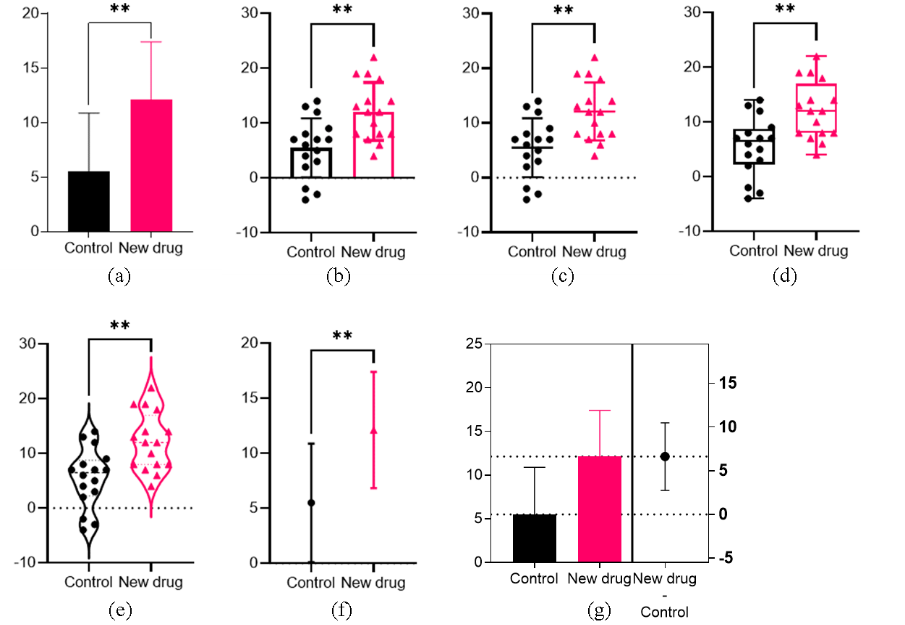
图1  成组t检验图形

 

配对t检验

 

配对t 检验，是单样本t检验的特例。配对t检验采用配对设计方法适用以下几种情形：

 

①配对的两个受试对象分别接受两种不同的处理；

②同一受试对象接受两种不同的处理；

③对同一受试对象处理前后的结果进行比较（即自身配对），如患病/服药前后某指标变化；

④对同一对象的两个部位给予不同的处理，如同一个体癌组织和癌旁组织的某基因表达。

 

在配对设计中，两组数据的个数相等，且一一对应，配对t检验适合绘制前后图（Before and After）。效果如图2所示

 

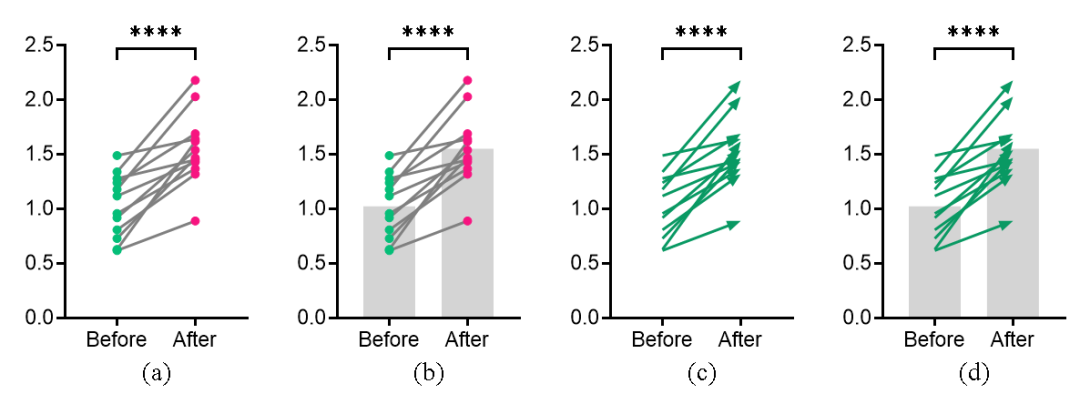
图2  配对t检验前后图

 

t检验针对的是两组计量资料的均数比较，如果是多于两组（k >2）样本的均数比较，则t检验将不再适用，而方差分析（Analysis of Variance，ANOVA）是解决这个问题的重要分析方法。

 

普通单因素方差分析

 

普通单因素方差分析，在方差分析中，普通单因素方差分析（Ordinary one-way ANOVA，也被称为完全随机设计的方差分析）的使用频率最高，因此本节重点介绍普通单因素方差分析，进行普通单因素方差分析的前提也需要独立样本符合正态分布和方差齐性。

 

如表1所示。一般而言，对于任意组别的两两比较，当比较的组数大于或等于4组时，推荐使用Turkey法进行多重比较；当比较的组数小于或等于3组时，Turkey法和Bonferroni法都可以使用；当试验组与对照组比较时，首选Dunnett法；当比较指定组别时，Bonferroni法最为常用，也可以使用Šídák法。

 

表1  单因素方差分析多重比较方法

 

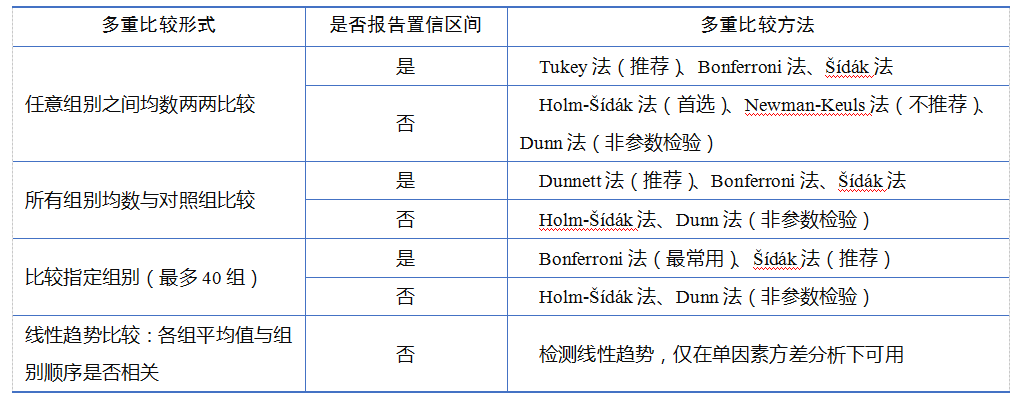
指定组别多重比较在组数较少时，可以采用“连线+标注”的形式即可，如图3所示。

 

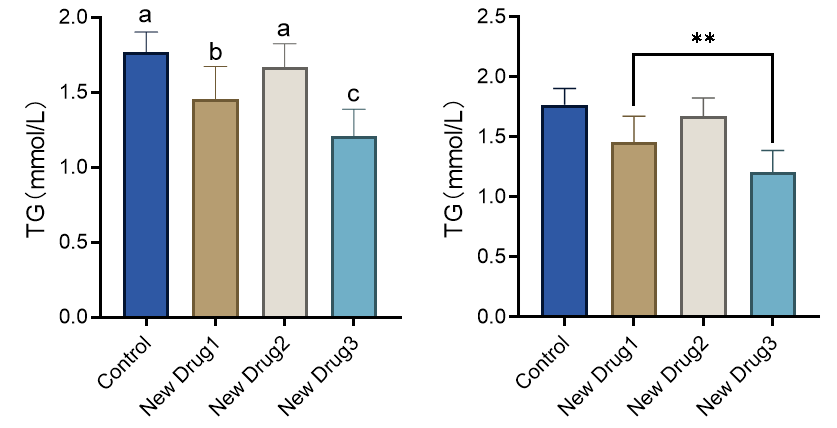
图3  任意组别（a）和指定组别多重比较（b）的柱状图

 

随机区组设计（Randomized block design）又被称为配伍设计，其做法是先将受试对象按照条件相同或相近组成m个区组（或者称为配伍块），且每个区组中有k个受试对象，再将其随机地分配到k个处理组中。

 

相比于完全随机设计，随机区组设计可以进行局部控制，将区组因素导致的变异分离出来，减少了随机误差，提高了试验效率。

 

随机区组设计的方差分析属于无重复数据的两因素方差分析，但是区组因素并不是令人感兴趣的试验因素，且区组因素与试验因素之间不存在交互作用。

 

重复测量单因素方差分析

 

重复测量单因素方差分析（Repeated measurement design）单因素方差分析中有一种特殊形式为重复测量设计，很容易与普通单因素方差分析混淆。

 

重复测量设计指同一受试对象的某一观测指标在不同时间点上进行多次测量的设计方法，在进行重复测量数据分析时有两种方法：

 

一种是重复测量方差分析（Repeated measures ANOVA），基于一般线性模型（General linear model，GLM），这种方法不能有缺失值（Missing values），如果有则不能进行处理和计算，需要把缺失值所在区组都删除；

 

另一种是混合效应模型（Mixed-effects model），这个模型别称很多，常见的有多水平模型（Multilevel model）、分层线性模型（Hierarchical linear model）、随机效应模型（Random effect model）等，这种方法可以处理缺失值，适用范围比重复测量方差分析更广。

 

ROC曲线

 

ROC曲线（Receiver operating characteristic curve，受试者工作特征曲线），又被称为感受性曲线（Sensitivity curve），是以真阳性率（灵敏度）为纵坐标，假阳性率（1-特异度）为横坐标绘制的曲线。

 

可以通过分别计算各个试验的ROC曲线下的面积（AUC）进行比较，哪一种试验的AUC最大，则哪一种试验的诊断价值最佳。

 

ROC曲线也是评估一个生物标志物、预测性能的有用图形工具。

 

例如可以将一个生物标志物组区分为两个群组（如试验组和对照组、存活和死亡、疾病和健康、癌症和癌旁），结合临床数据，可以验证某个基因或模型是否可以作为疾病诊断和预后标志物。效果如图5、图6所示

 

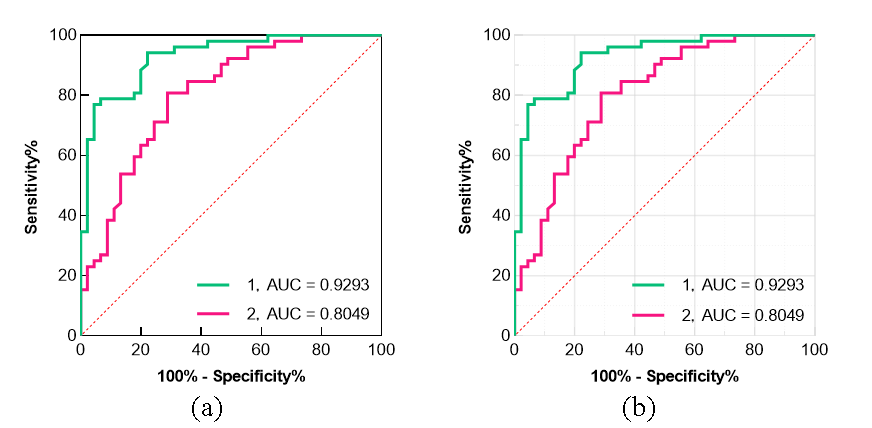
图4  叠加ROC曲线

 

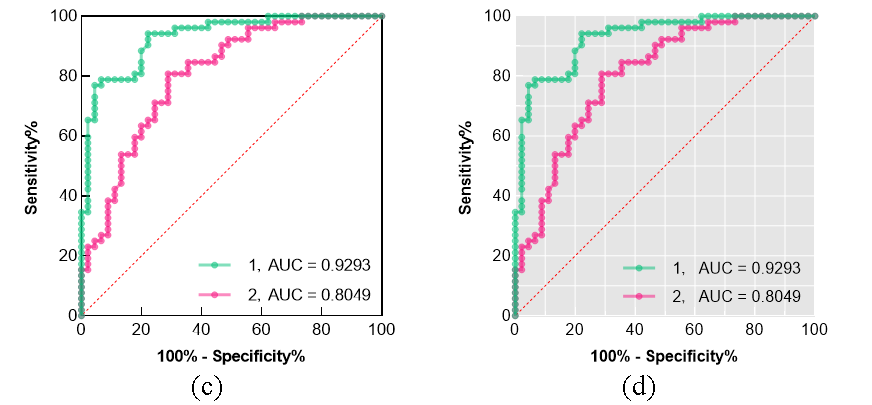
图5  叠加ROC曲线（续）

 

Bland-Altman图

 

Bland-Altman图，Bland-Altman分析最初是由Bland JM和Altman DG于1986年提出的，用于比较两个计量资料之间的一致性。建立多个数学模型后，有时还需要探讨这些检验方法的一致性，如对比两种方法或仪器诊断结果是否一致。

 

通过对两种方法进行一致性评价，可以回答“这两种方法能否互相替代”这样的问题。效果如图7所示

 

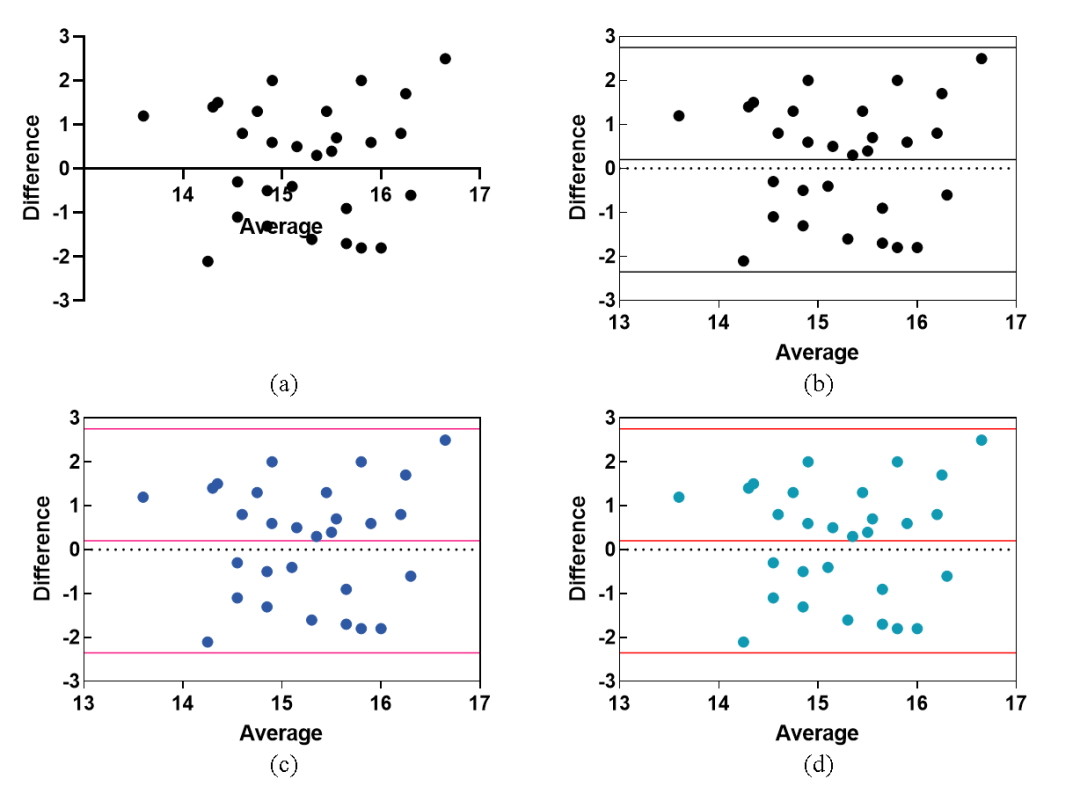
图6  Bland-Altman图

 

本文摘编自《GraphPad Prism学术图表（全彩）》