【摘要】 半导体器件中载流子输运的数值模拟可以追溯到Scharfetter和Gummel[1]的著名工作，他们提出了一种至今仍在使用的DD方程的稳健离散化。

在半导体技术最开始的时候，可以使用依赖于漂移扩散（DD）形式的简单分析模型来估计电气器件特性。必须进行各种近似才能获得闭合形式的解决方案，但最终的模型捕捉到了设备的基本特征。这些近似包括简化的掺杂分布和器件几何形状。随着技术的不断完善和改进，这些近似值失去了基础是必需的。这个目标可以通过数值求解DD方程来实现。半导体器件中载流子输运的数值模拟可以追溯到Scharfetter和Gummel[1]的著名工作，他们提出了一种至今仍在使用的DD方程的稳健离散化。

 

为了克服DD模型的一些局限性，已经提出了扩展，基本上增加了平均载波能量的额外平衡方程。此外，将附加的驱动项添加到与载流子温度的梯度成比例的电流关系中。然而，这些模型中存在大量，它们之间的关系也存在相当大的混乱。本文的目的是澄清各种模型之间的重要区别和相似之处。为了掌握这项任务，需要更仔细地研究各种推导，其中突出了要点。然后对最重要的模型进行总结和评估，然后对推导中的假设进行批判性讨论。

 

然而，对于快速增加的电场，平均能量落后于电场，局部平衡的假设变得无效。滞后的结果是，最大能量可能比局部能量平衡方程预测的能量小得多。载流子温度的这种非局部性如图所示。1（a）对于具有不同沟道长度的n-n-n结构，其中空间坐标已被归一化，以使所有器件的电场分布重叠。所选择的偏压在所有器件中都能产生300 kV/cm的最大电场。这种行为的一个重要后果是，平均能量的滞后导致载流子速度的过冲，如图所示。第1（b）段。还显示了饱和速度，这是在静态体积测量中观察到的最大速度。速度过冲的原因是迁移率取决于一阶平均能量，而不是电场。由于迁移率尚未被增加的能量降低，但电场已经很大，因此观察到速度上的过冲，直到载流子能量再次与电场达到平衡。

 

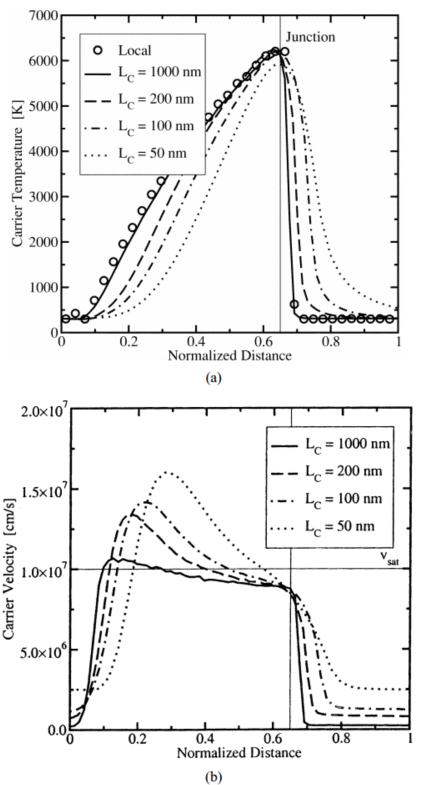
图1 具有不同沟道长度的可比n-nn结构的载流子温度

 

Kane表达式的不同拟合的比较如图2所示，以及Fischetti和Laux[2]使用的状态的数值密度。当拟合到低能范围eV时，和当拟合到高能范围eV，其中具有不寻常的eV尺寸。对于，形状由凸变为凹；因此，低能量或高能量范围都可以适当地拟合，但不能同时拟合。由于评估分布函数的矩需要色散关系，这需要在整个能量范围内进行积分，因此需要一个小于1的值来准确拟合低能量区域，因为这是它的最大值。然而，由此产生的态密度显示出“抛物线状”行为；因此，它对于描述非抛物型输运现象的价值是有限的。

 

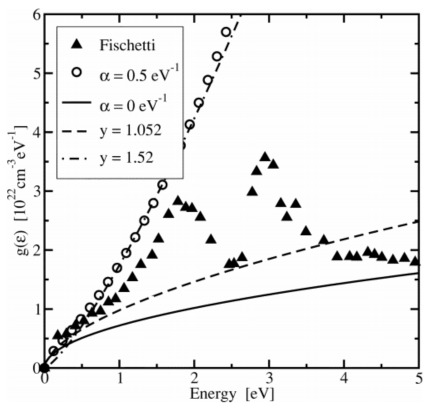
图2 状态密度的不同表达式的比较

 

[1] D. L. Scharfetter and H. K. Gummel, “Large-signal analysis of a silicon read diode oscillator,” IEEE Trans. Electron Devices, vol. ED-16, pp. 64–77, Jan. 1969.

[2] M. V. Fischetti and S. E. Laux, “Monte Carlo analysis of electron transport in small semiconductor devices including band-structure and space-charge effects,” Phys. Rev. B, vol. 38, no. 14, pp. 9721–9745, 1988.

 

科学指南针以分析测试为核心，提供材料测试、环境检测、生物服务、模拟计算、科研绘图等多项科研产品，累计服务1800+个高校、科研院所及6000+家企业，获得了60万科研工作者的信赖。始终秉持“全心全意服务科研，助力全球科技创新”的使命，致力于为高校、院所、医院、研发型企业等科研工作者提供专业、快捷、全方位的服务。

 

免责声明：部分文章整合自网络，因内容庞杂无法联系到全部作者，如有侵权，请联系删除，我们会在第一时间予以答复，万分感谢。