【摘要】 在本文开发并初步验证了一个详细的有限元模型，该模型模拟了圆柱在平面微动试验中的摩擦接触行为。

微动磨损是一种表面退化过程，其中材料的去除是由接触部件之间的小振幅振荡运动引起的，如柔性联轴器和花键、关节结构等。对这种类型的表面损伤机制的分析已经得到了广泛的发展。据报道，影响微动磨损的主要参数是法向载荷、滑移幅度、频率、接触几何形状、表面粗糙度和材料性能。Vincent等人[1]建立的“微动图谱”方法表明，微动损伤的演变在很大程度上取决于微动状态。碎屑也是影响微动磨损的关键因素。据报道，一旦碎屑积聚在接触表面并形成致密的氧化层，磨损率就会显著降低。近年来，Godet[2]发展了第三体摩擦学和速度调节机制的理论，以解释磨损碎片在特定微动条件下的作用。

 

与定性认识的发展相比，微动磨损的定量评估还不够先进。其中一个困难是缺乏一个“通用”且制定良好的磨损模型。此外，还不清楚如何将磨损碎片的影响纳入这样一个定量模型中。对于某些情况，在磨损碎屑更容易从接触区域消除并且保持更多金属与金属接触的情况下，可以合理地忽略碎屑的影响。在这种情况下，微动磨损因此可以被视为纯粹基于接触的磨损问题。Korovchinsky等人[3]提出了一种分析方法来模拟二维赫兹构型在部分滑移条件下的微动磨损。在该模型中，局部应用Archard方程来评估一个循环中滑动区内的磨损和间隙变化。然后采用逐步过程来计算作为磨损循环次数增加的函数的接触特性的演变。

 

在本文开发并初步验证了一个详细的有限元模型，该模型模拟了圆柱在平面微动试验中的摩擦接触行为。微动试验使用交叉圆柱平面布置进行，如图1所示。圆柱形试样的直径为12mm。扁平试样牢固地固定在机器的底座上；圆柱形试样由电磁振动器驱动。安装在试样支架上的线性可变位移传感器监测施加的行程。除了需要手动调整的初始阶段外，冲程在整个测试过程中自动保持恒定。正常负载是通过一个杠杆由自重施加的。在试验过程中，切向摩擦力通过连接在驱动臂上的应变仪进行测量。

 

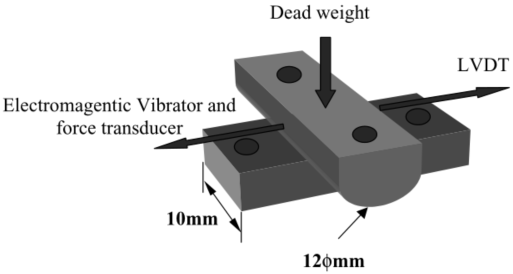
图1 圆形与平面交叉试样排列示意图

 

图2显示了在不同（正常）接触载荷下，COF随磨损循环次数的变化。COF增加，特别是在185和500N的正常负载下。当磨损循环次数超过2000次循环时，COF趋于稳定值。最初的低COF可归因于表面氧化物膜的存在。一旦氧化膜被消除，金属-金属和/或金属磨损颗粒的相互作用就会开始，促进COF的大幅增加。从图3中还发现，稳定的COF随着正常负载的增加而降低。具体而言，185N正常负载下的COF最高，为≈0.8。当正常负载分别增加到500和1670N时，它分别降低到0.75和0.6。这一趋势与之前的观察结果一致[19]，并归因于界面剪应力是常数值τ0的函数，也是平均接触压力p和界面剪切应力系数γ的乘积[20]。

 

图2 摩擦系数与微动磨损循环次数的关系。50μm；频率20Hz

 

[1] L. Vincent, Y . Berthier, M. Goget, Testing methods in fretting fatigue: a critical appraisal, ASTM STP 1159 (1992) 23–32.

[2] M. Godet, The third-body approach: a mechanical view of wear, Wear 100 (1984) 437–452.

[3] I.G. Korovchinsky, P .T. Rajeev, T.N. Farris, Wear in partial slip contact, J. Tribol. 123 (2001) 848–856.

 

科学指南针充分发挥互联网技术和业务优势，在国内率先打造出业界领先的线上化、数字化的科研服务基础设施，在行业内首创用户自主下单、服务全流程追踪、测试“云现场”等模式，进一步提高了大型科学仪器设施开放共享和使用效率，以实际行动助力科技创新。现已发展成为中国专业科研服务引领者，已获得检验检测机构资质认定证书（CMA）、实验动物使用许可证、“ISO三体系认证”等专业认证。

 

免责声明：部分文章整合自网络，因内容庞杂无法联系到全部作者，如有侵权，请联系删除，我们会在第一时间予以答复，万分感谢。