【摘要】 通常能够影响相稳定性的变量是温度和压力。

通常能够影响相稳定性的变量是温度和压力。然而，电场对吉布斯自由能也有作用。事实上，电场在材料处理和合成过程中有着广泛的应用。但作为一种新的能量形式，电场的作用机理尚不清楚，如果应用电场来研究微观状态下吉布斯自由能的变化趋势，将有助于研究材料中电场的作用机理。

托马斯-费米模型在分子论、固体理论等领域有着广泛的应用。利用它来研究原子系统的吉布斯自由能是电子密度n(r)的计算，这也是FNST原理的关键因素。TTUS可以通过电荷密度与内电势之间的关系来研究。电荷密度为

 

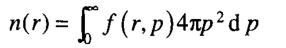
其中p是电子的动量，r是电子的位置，f(r，p)是电子的费米分布函数。

 

 

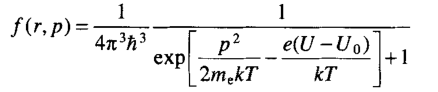
其中静电电荷e=4.80×10-10单位，A是普朗克常数，Me是电子的有效质量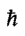，是玻尔兹曼常数，me是原子中电子的最大能量，k是玻尔兹曼常数，-eUo是原子中电子的最大能量，U=U(r)是r的势能。

 

 

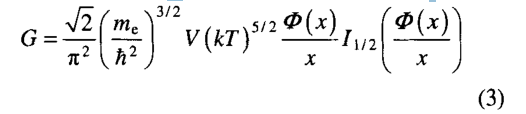
Thomas-Fermi模型采用部分自由电子气近似，可以部分表示自由电子气的吉布斯自由能。同时可以在原子体积范围内引入相关性，然后积分，从而得到TF 模型的吉布斯自由能：

 

 

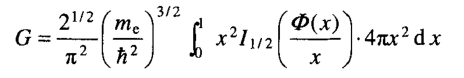
其中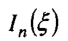，是费米函数，x=r/ro，而ro是原子的半径。

 

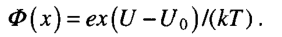
TF模型的温度边界条件如下：

 

 

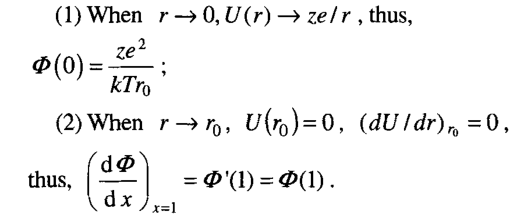
当原子系统不处于基态时，原子的边界条件会发生相应的变化。在本篇文章中，电场的影响并没有改变原子结构的主要部分，即原子的原子核和局域电子，而是扰乱了自由电子（改变了电子密度）。TF模型描述的系统仍然服从基本关系，但必须修改边界条件。