【摘要】 为此,引入了总是存在的测度外态密度,并给出了测度态密度存在时的上界
研究Schrödinger算子的态密度,如图1所示[1]。其中Κ是拉普拉斯算子,V是有界势。一个区间的状态密度测量给出了“每单位体积的状态数” 在区间中有能量;它的累积分布函数是状态的积分密度。状态测度的有限体积密度,即Schrödinger算子对有限体积的限制的状态测度密度,总是定义良好的。状态测度的密度由状态测度的有限体积密度的适当极限给出,当这种极限存在时。已知这些极限存在于Schrödinger算子,其中势V在某种意义上在空间中是均匀的(例如,周期势,遍历Schrödinger算子),但不存在于一般的Schrödinger算子。对于一般Schrödinger算子,不能定义状态测度的密度和相应的状态积分密度。
为此,引入了总是存在的测度外态密度,并给出了测度态密度存在时的上界。我们证明了小区间外测度状态密度的上界,建立了Schrödinger算子在一维、二维和三维以及离散Schrödinger算子在任意维上的log-Hölder连续性。对于周期的和遍历的Schrödinger算子,态的密度ηψ可以在适当的意义上定义为态的有限体积密度ηΛ的弱极限,对于盒子Λ→Rd的序列ψ。在这种情况下,态的积分密度Nψ(E):= ηψ(]−∞,E])满足Nψ(E) = limΛ→Rd NΛ,ψ(E),除了一个可数的能量集。而且,它们都是重合的,所以我们用η(B):= ηψ(B)和N(E):= Nψ(E)来定义态的密度测量η和态N(E)的积分密度。
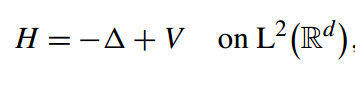
图1. 态密度公式 [1]
由于一般Schrödinger算子无法定义状态测度的无限体积密度和状态的积分密度,因此定义了Rd的Borel子集B上的状态测度外密度(图2)。它们在有界集合上总是有限的。已发表的结果似乎仅限于存在态的积分密度的情况。对于周期势,态的积分密度的连续性等价于特征值的不存在,这是Thomas证明的一个非平凡结果。对于遍历Schrödinger算子,状态的积分密度的连续性等价于能量的不存在性,这种能量是概率为1的无限多重特征值。
虽然Schrödinger算子可以具有无限多重的特征值,但很难想象对于几乎所有遍历Schrödinger算子的实现,固定能量如何成为无限多重的特征值。Craig和Simon证明了一维遍历Schrödinger算子[6]和任意维遍历离散Schrödinger算子的状态积分密度的log-Hölder连续性(指数为1)。Delyon和Souillard提供了离散情况下状态的积分密度连续性的简单证明。但是,对于多维(连续)遍历Schrödinger算子,状态的积分密度的连续性,虽然是预期的,但很难得到全面的证明。
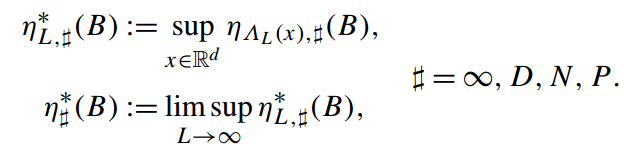
图2. 定义的状态测外密度[1]
[1] Bourgain, J., Klein, A. Bounds on the density of states for Schrödinger operators. Invent. math. 194, 41–72 (2013).
科学指南针充分发挥互联网技术和业务优势,在国内率先打造出业界领先的线上化、数字化的科研服务基础设施,在行业内首创用户自主下单、服务全流程追踪、测试“云现场”等模式,进一步提高了大型科学仪器设施开放共享和使用效率,以实际行动助力科技创新。现已发展成为中国专业科研服务引领者,已获得检验检测机构资质认定证书(CMA)、实验动物使用许可证、“ISO三体系认证”等专业认证。
免责声明:部分文章整合自网络,因内容庞杂无法联系到全部作者,如有侵权,请联系删除,我们会在第一时间予以答复,万分感谢。











 您已经拒绝加入团体
您已经拒绝加入团体

 2024-08-20
2024-08-20
 2515
2515
 0
0










